
Презентация "Усеченная пирамида"

Краткое описание документа:
В презентации «Усеченная пирамида» продолжается изучение многогранников - ученики знакомятся с определением усеченной пирамиды и ее основными свойствами.
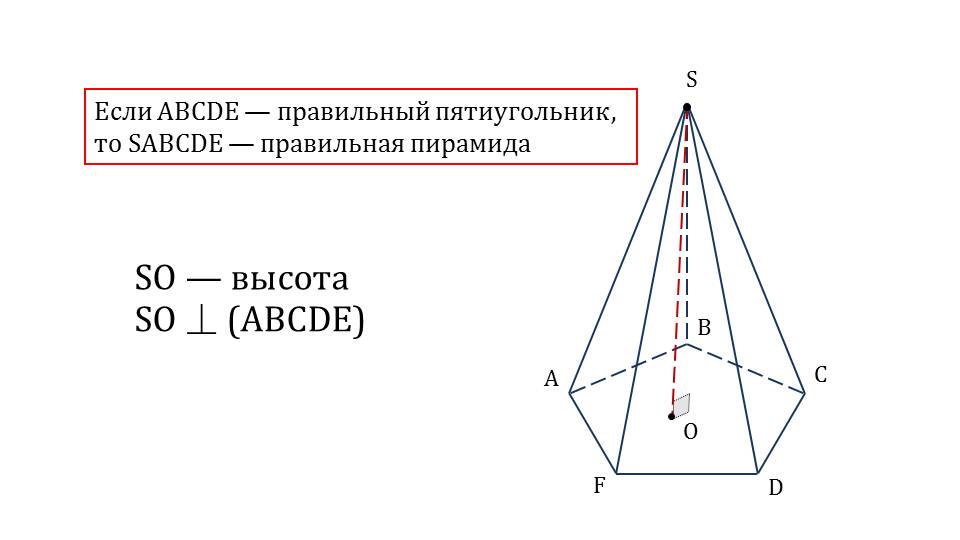
Урок начинается с того, что учитель напоминает о правильной пирамиде – на рисунке изображена пирамида и ее высота, которая перпендикулярна плоскости основания пирамиды.
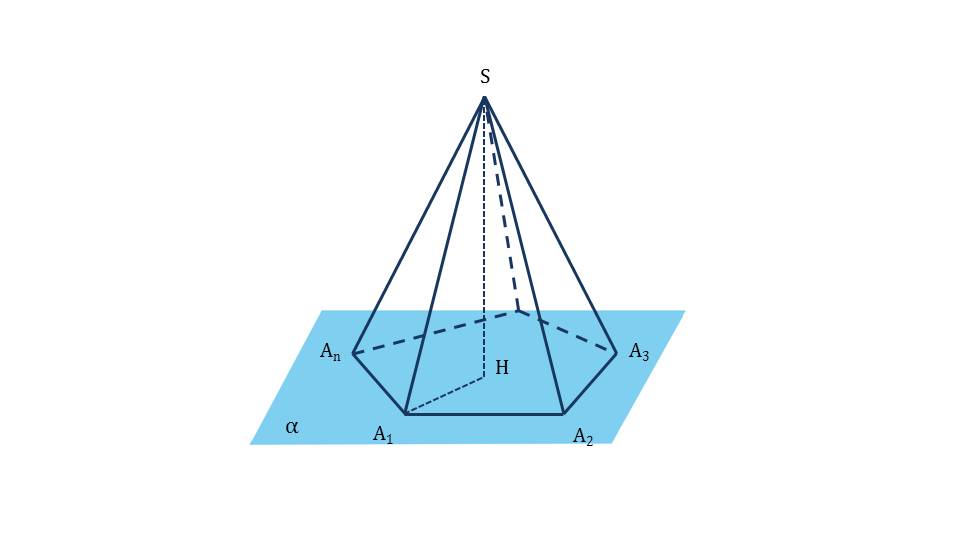
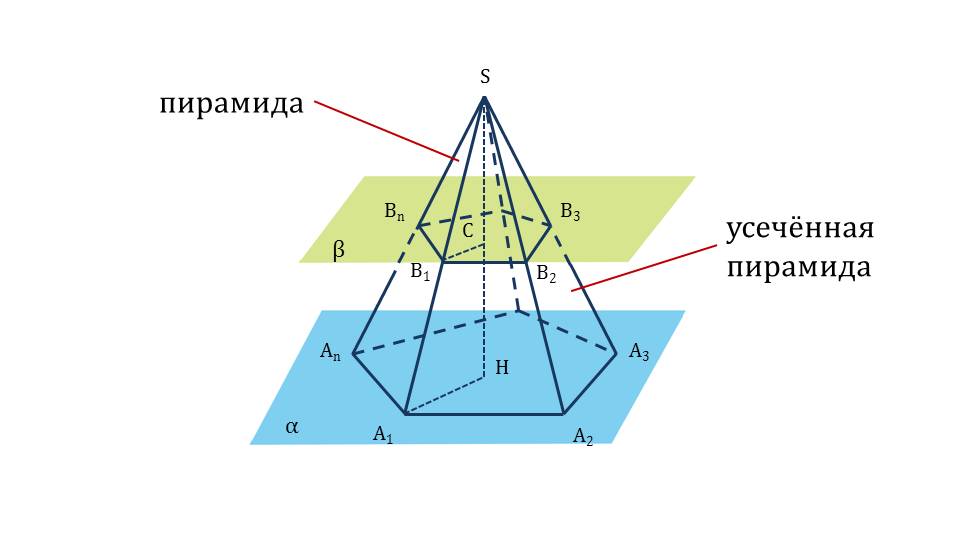
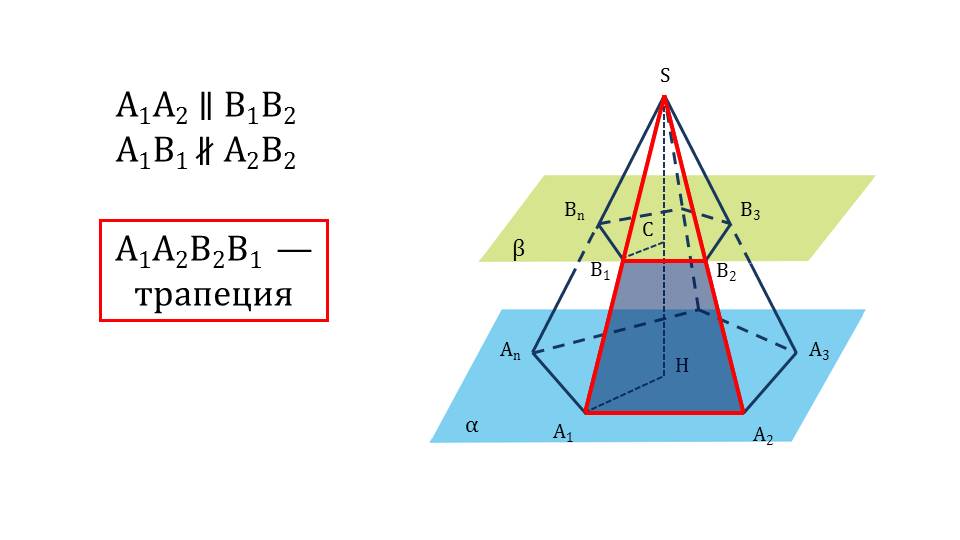
Чтобы построить усеченную пирамиду, в правильной пирамиде проводят сечение – плоскость, параллельную основанию (слайды 3, 4). Эта плоскость разбивает правильную пирамиду на 2 фигуры: на пирамиду, подобную исходной, и усеченную пирамиду. На рисунке (слайд 5) показана усеченная пирамида, ее основания, боковые ребра и грани, высота. Автор представил фигуру максимально наглядно, чтобы акцентировать внимание учащихся на основных понятиях пирамиды, которые будут использоваться при решении задач.
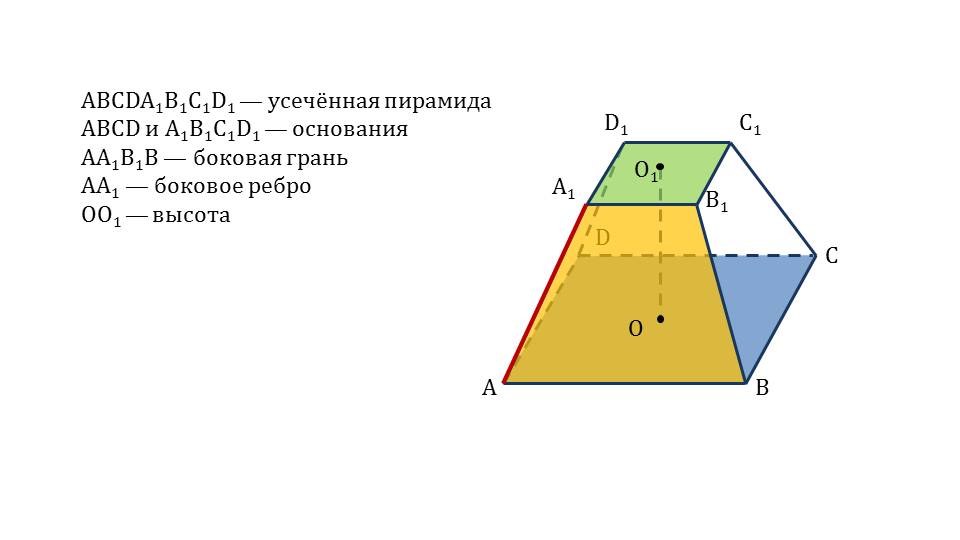
Далее рассматриваются основные свойства усеченной пирамиды, их также необходимо хорошо изучить и запомнить:
- боковые грани усеченной пирамиды являются трапециями;
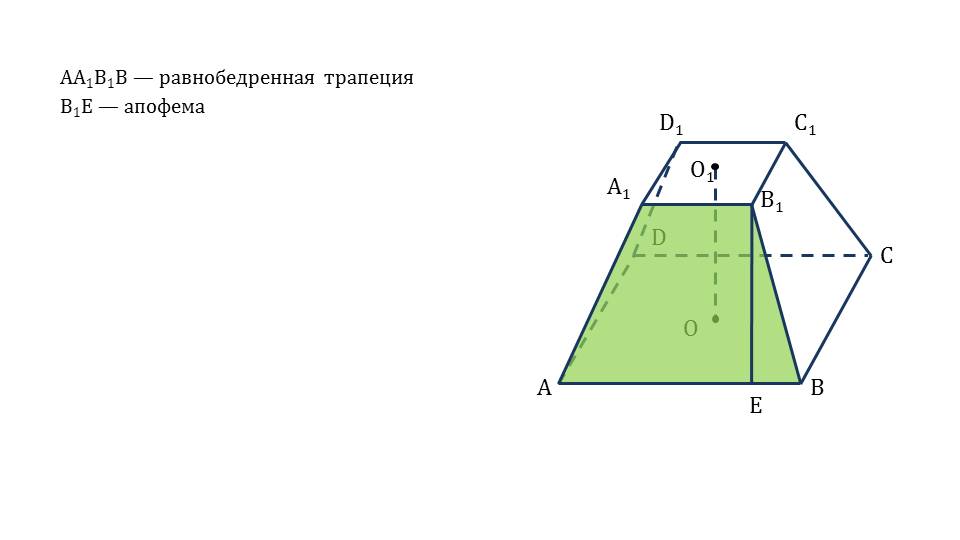
- боковые грани правильной усеченной пирамиды - равнобедренные трапеции, равные между собой;
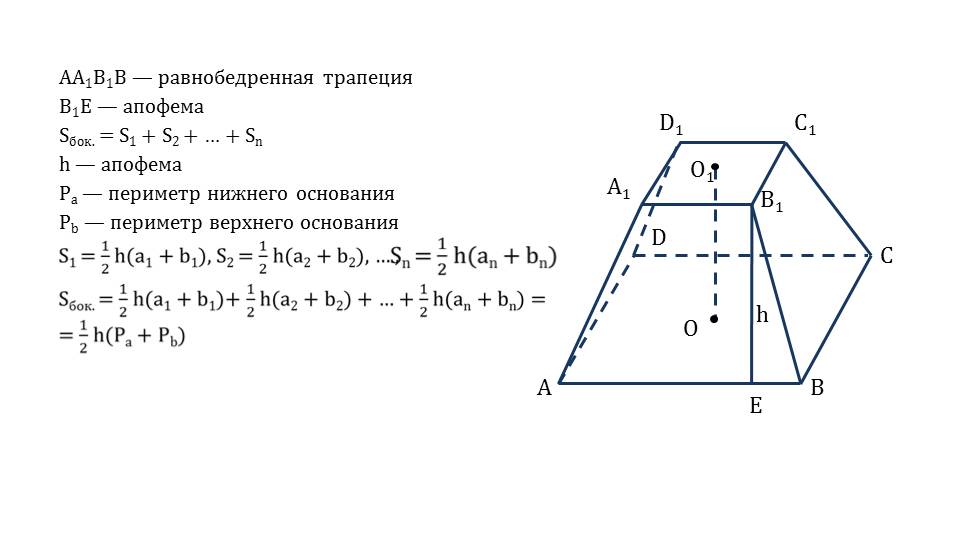
- апофема усеченной пирамиды – это высота равнобедренной трапеции.
Приводится формула, по которой с помощью периметров оснований и апофемы можно рассчитать площадь боковой поверхности правильной усеченной пирамиды.
Изучив теоретическую часть, школьники могут приступить к выполнению практических заданий. В презентации предложена задача по нахождению высоты и апофемы усеченной пирамиды.
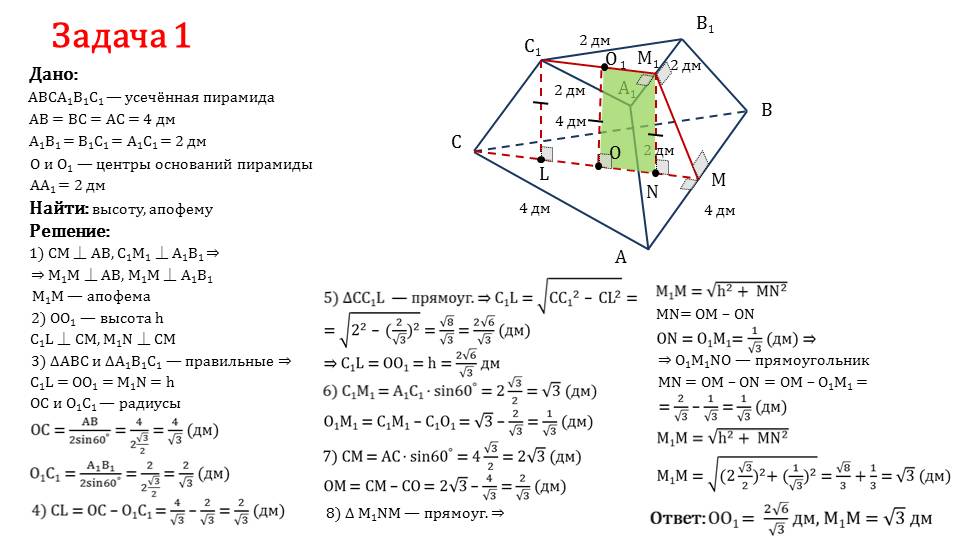
В задаче известны: длины сторон оснований, длина бокового ребра. При решении важно правильно построить чертеж, исходя из данных задачи, автор уделяет этому особое внимание. Определяется нахождение апофемы и высоты пирамиды на чертеже. Далее делается вывод, что треугольники, которые являются основаниями пирамиды, правильные; определяются и находятся по формулам радиусы описанных окружностей этих треугольников. Используя размеры радиусов при рассмотрении прямоугольного треугольника, где неизвестная высота пирамида является катетом, производят вычисление высоты.

При рассмотрении другого прямоугольного треугольника, где искомая апофема пирамиды является гипотенузой, можно найти ее длину, так как все данные для определения размеров двух других сторон этого треугольника уже получены ранее.
Данная презентация может быть применена учителем на уроке геометрии или при дистанционном обучении, а также может быть самостоятельно изучена и проработана учениками, так как включает в себя основные теоретические моменты и, что немаловажно, практическую часть – детальное решение задачи.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8710 |
| Номер материала | 903 |