
Презентация "Вычисление объемов тел с помощью определенного интеграла"

Краткое описание документа:
В предыдущих презентациях мы познакомились с понятием объема тела и научились находить объем прямоугольного параллелепипеда, призмы, цилиндра. В данной презентации для 11-го класса ученики узнают о еще одном способе вычисления объемов тел – с помощью определенного интеграла.

Вначале презентации автор приводит формулу определенного интеграла Ньютона-Лейбница. На следующем слайде приводится основная формула вычисления объемов тел с помощью определенного интеграла с доказательством.

Допустим, что дана функция Ф (x) на отрезке от а до b в плоскости координат. Допустим также, что эта функция положительна и непрерывна.
Проведены две плоскости α и β таким образом, что α параллельна β, а ось Оx перпендикулярна плоскости α. Необходимо найти объем тела, полученного вращением вокруг оси Оx функции Ф (x). На рисунке мы видим, что а и b – это абсциссы точек пересечения оси Оx с плоскостями α и β, причем a < b. Ф (x) – это плоскость сечения. Площади сечений запишем как S (x) = S (xi), Разделим интервал от a до b на n частей: a = x0, b = xn. Укажем, чему будет равно расстояние между каждым xi, оно будет равно (b – a)/ n. Обозначим тело, вращаемое вокруг оси Оx, как Т. Тело вращения Т ограничено поверхностью вращения и плоскостями α и β, другими словами тело Т находится между Ф (xi-1) и Ф (xi). Объем тела вращения Т равен сумме объемов составляющих его тел. Тогда объем каждого составляющего тела мы можем записать как площадь каждой фигуры S (xi), умноженной на расстояние между каждым xi. Далее по описанию в презентации вы увидите, как выводится формула объем тела, полученного вращением, с помощью определенного интеграла.
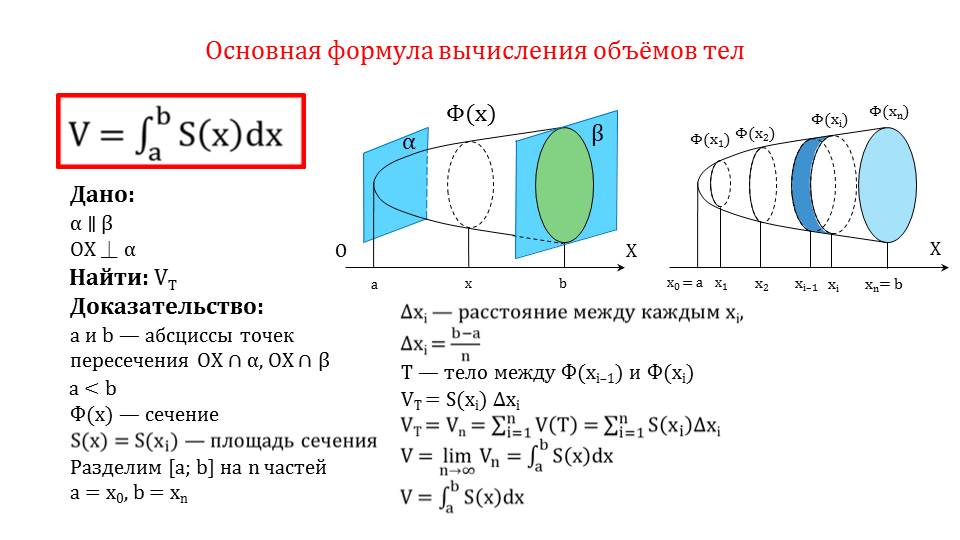
Мы пришли к выводу, что определенный интеграл имеет геометрический смысл: это площадь криволинейной трапеции, которая ограничена линиями функции Ф (x) на интервале от a до b при y = 0.
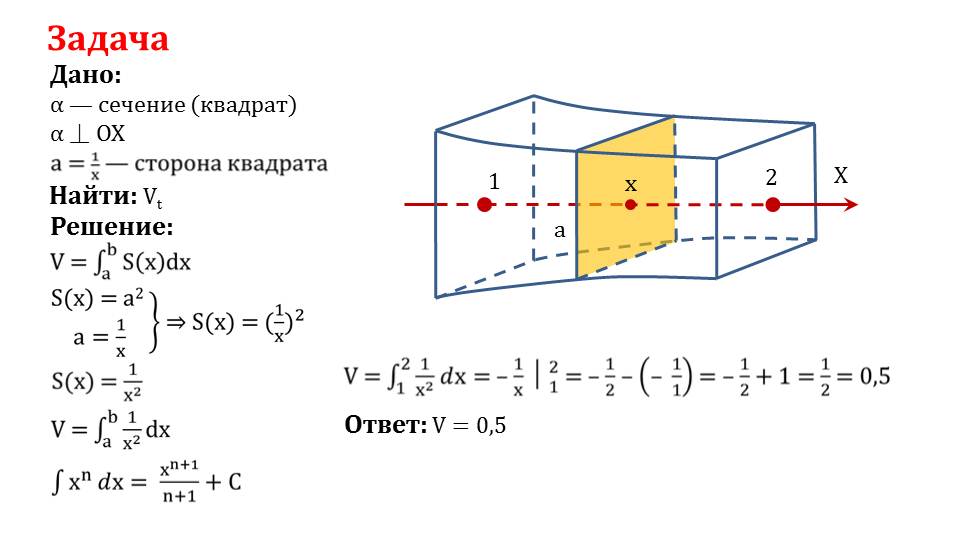
Перейдем к задаче. Дано геометрическое тело, где известно, что плоскость α – сечение в форме квадрата, это сечение перпендикулярно OX, сторона квадрата равна а = 1/x. Необходимо вычислить объем данного тела. Сделаем схематический рисунок задачи. Напишем формулу вычисления объема тела с помощью определенного интеграла. Найдем площадь S (x) = a2, т.к. мы знаем, что данная фигура квадрат. S (x) = (1/x)2 = 1/x2. Подставив найденное значение S (x) = 1/x2 в формулу объема, сможем вычислить интеграл и найти, что объем данного геометрического тела будет равен 0,5.
Таким образом, в нескольких темах мы изучили, по каким формулам можно найти объемы различных тел – прямоугольного параллелепипеда, призмы, цилиндра; а также узнали, как можно вычислить объем тела с помощью определенного интеграла.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9483 |
| Номер материала | 981 |