
Презентация "Взаимное расположение сферы и плоскости"

Краткое описание документа:
В предыдущих уроках рассматривалась такая фигура, как сфера. Изучались такие основные параметры, как радиус, центр, диаметр. Выводилось также уравнение сферы.

Так как сфера рассматривается в пространстве, ее можно изучить с точки зрения взаимного расположения с плоскостью.
Данная презентация посвящена изучению темы – взаимное расположение сферы и плоскости. На первом слайде приводится сфера и уже выведенное в предыдущем уроке уравнение.
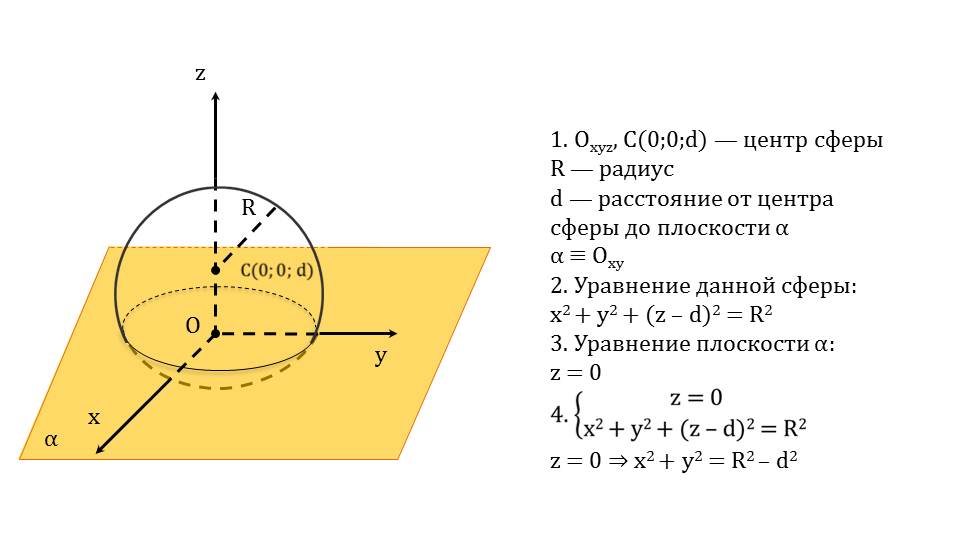
Любая сфера может быть усечена плоскостями. Зная уравнение сферы можно записать уравнение плоскости, которая ее пересекает.
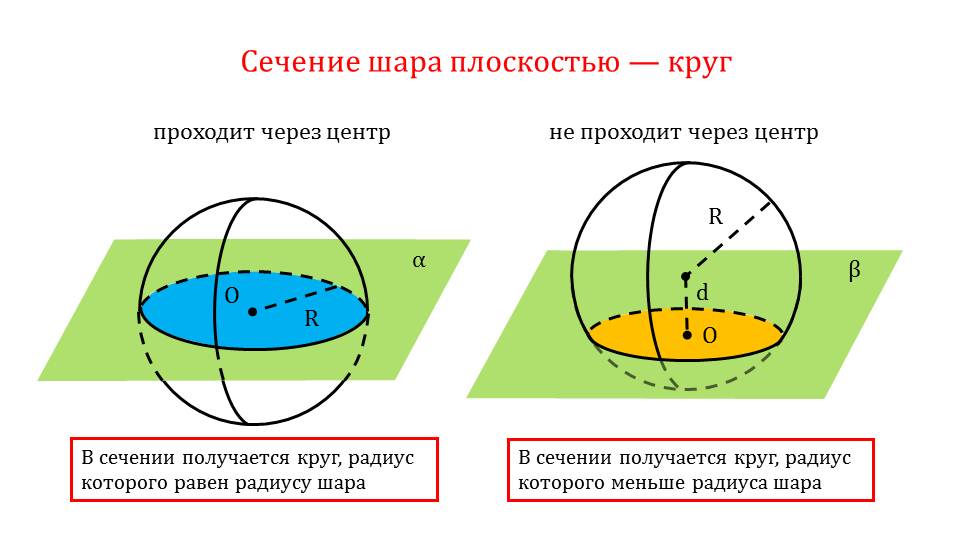
Если плоскость будет проходить через центр шара, то мы получим окружность с радиусом, равным радиуса шара. Если же нет, то радиус будет являться меньше радиуса шара.
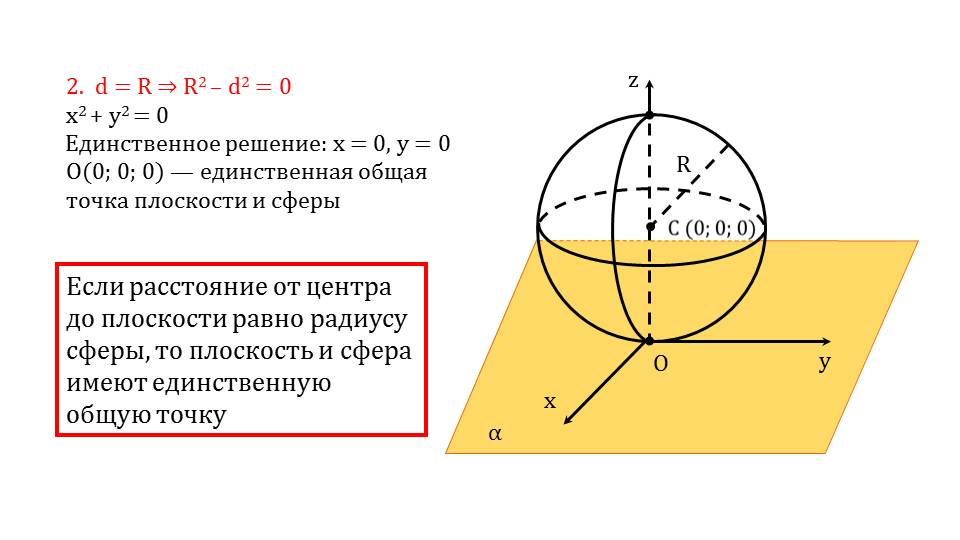
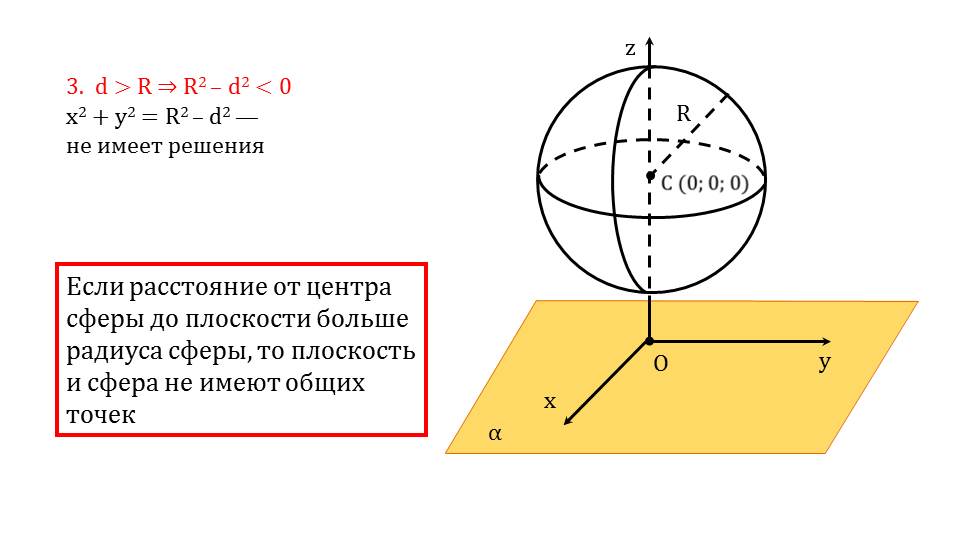
Если расстояние от центра окружности до плоскости равняется радиуса, то шар и плоскость будут иметь единственную общую точку. Если расстояние больше, чем радиус, то нетрудно догадаться, что плоскость и шар не имеют ни одной общей точки. Иными словами можно сказать, что плоскость и шар не пересекаются, не создают секущих.
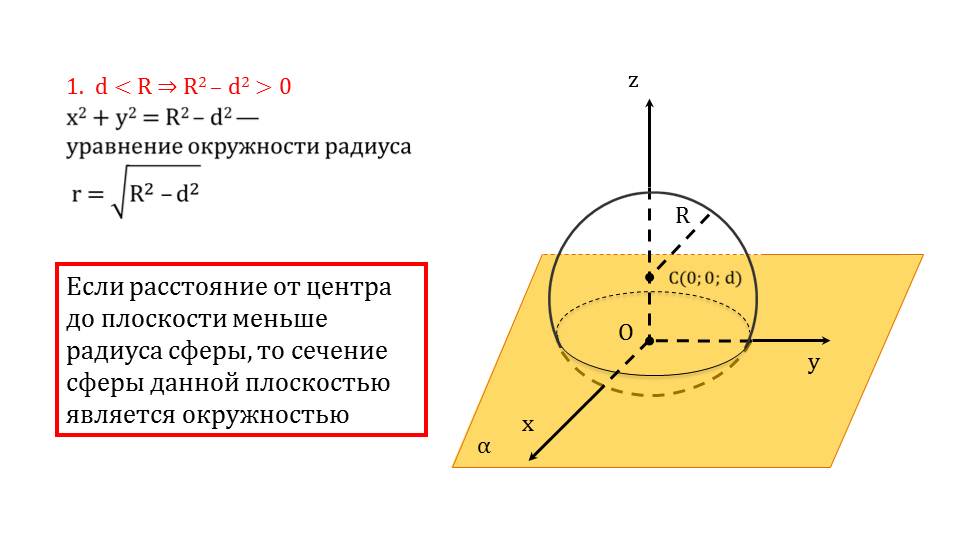
Если расстояние от центра до плоскости меньше, чем радиус, это говорит о том ,что плоскость и шар имеют бесконечное количество общих точек, то есть сфера и плоскость пересекаются.
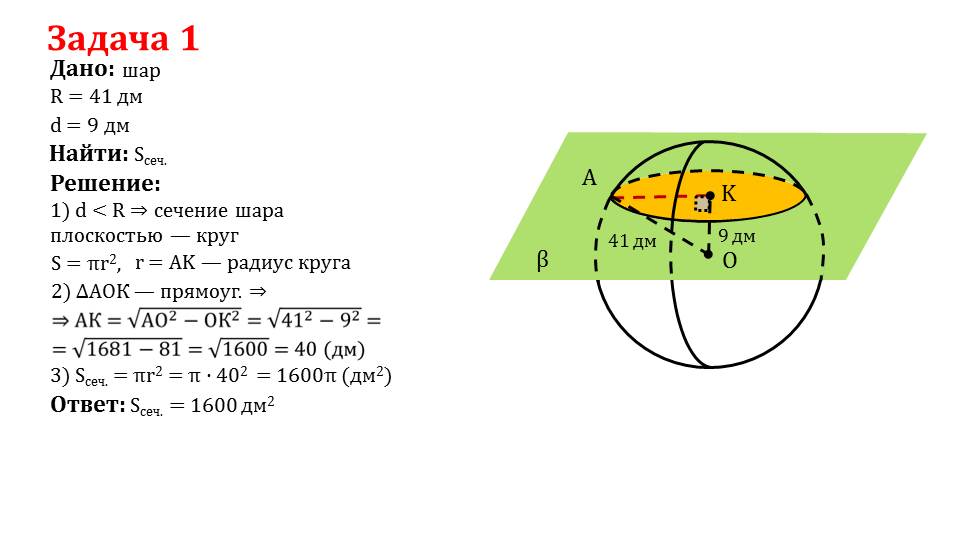
На последнем слайде, приводится рассмотрение задачи. На примере подобной задачи можно разобраться с принципом решения иных подобных задач в стереометрии.
Задача имеет подробное пошаговое описание. Рассмотреть ее лучше всего стоит с учителем или репетитором, если у школьника плохо развито пространственное мышление.
Данная презентация поможет провести очень полезный и наглядный урок, с помощью которого ученикам будут понятны и теория, и практика.
Если в школе есть возможность демонстрировать презентации параллельно с уроком, то он стане более эффективным и интересными для учеников.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8151 |
| Номер материала | 974 |