
Урок "Рациональные уравнения как математические модели реальных ситуаций" часть 2

Краткое описание документа:
В предыдущем видеоуроке вы ознакомились с основными азами темы. Продолжим рассмотрение и решение примеров.
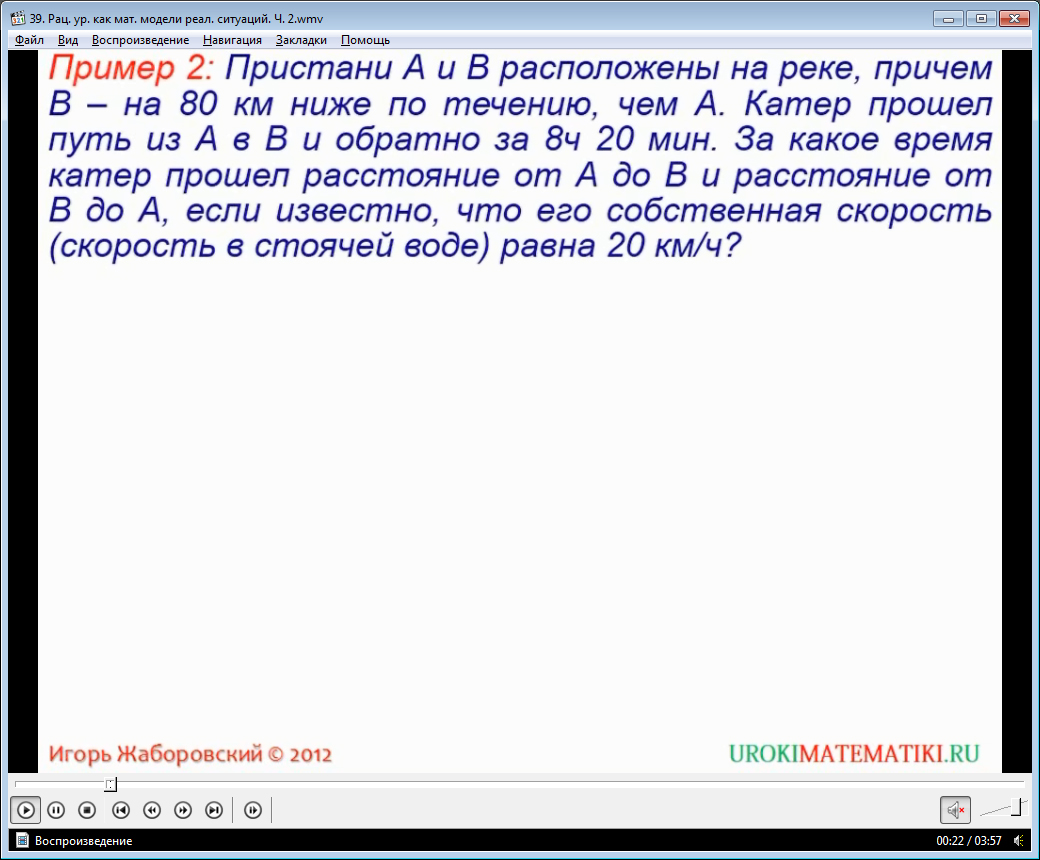
Задача. На озере расположены пристани D и C. Известно, что пристань C расположена на 60 км ниже D по течению. Моторная лодка прошла путь из D в C и обратно за 6ч 10 мин. За какой промежуток времени моторная лодка пройдёт расстояние от D до C и от D до C, если известно, что её собственная скорость (в стоячей воде) – 15 км/ч?
Решение
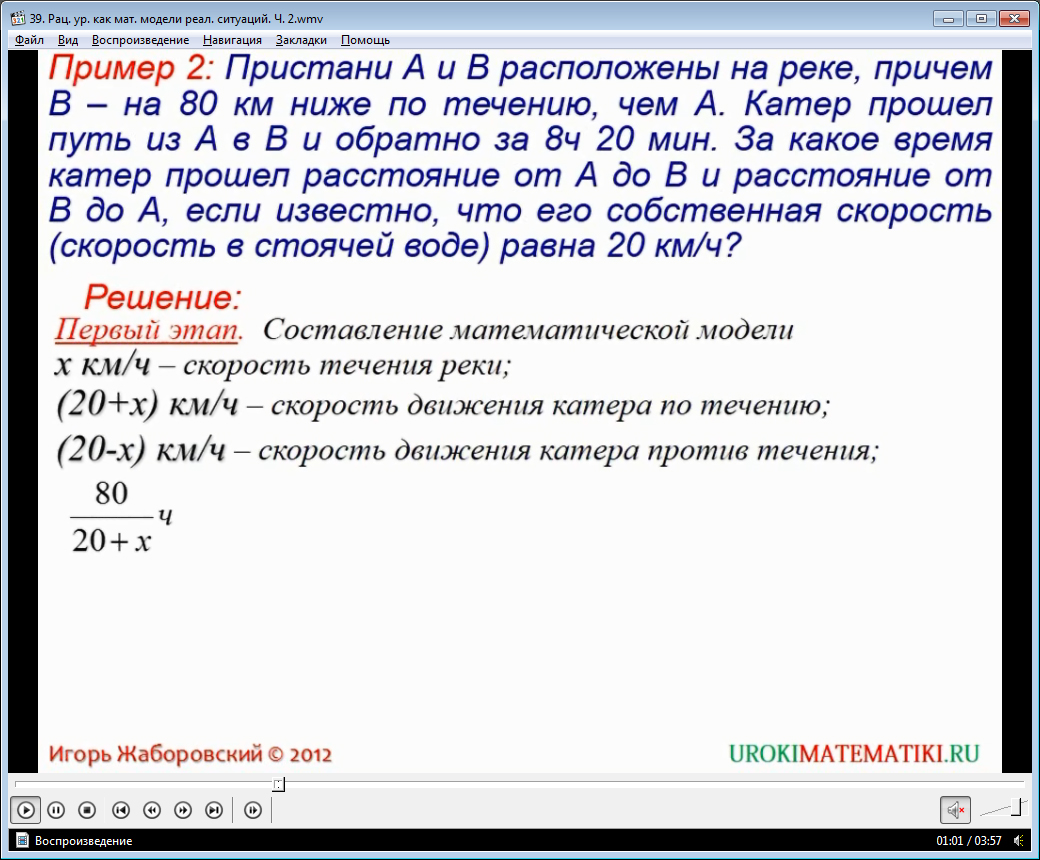
Построим решение задачи в несколько этапов.
Построение математической модели.
Пусть x км/ч – скорость течения озера. Тогда: (15+х) км/ч – скорость движения моторной лодки по течению, а (15-х) км/ч – скорость движения моторной лодки против течения.
60/15 + х- время движения моторной лодки по течению, 60/15 - х - время движения моторной лодки против течения.
По условию, на весь путь туда и обратно моторная лодка затратила 6 ч 10 мин, то есть 6 целых 1/6 ч или 37/6 ч. Но время, затраченное моторной лодкой на путь из D в C и обратно: ((60/15 + x)) + (60/15 - x)) ч.
Получим рациональное уравнение: (60/15 + х) + (60/15 - х) = 37/6.
Таким образом, можно составить математическую модель задачи, тем самым переведя её на математический язык.
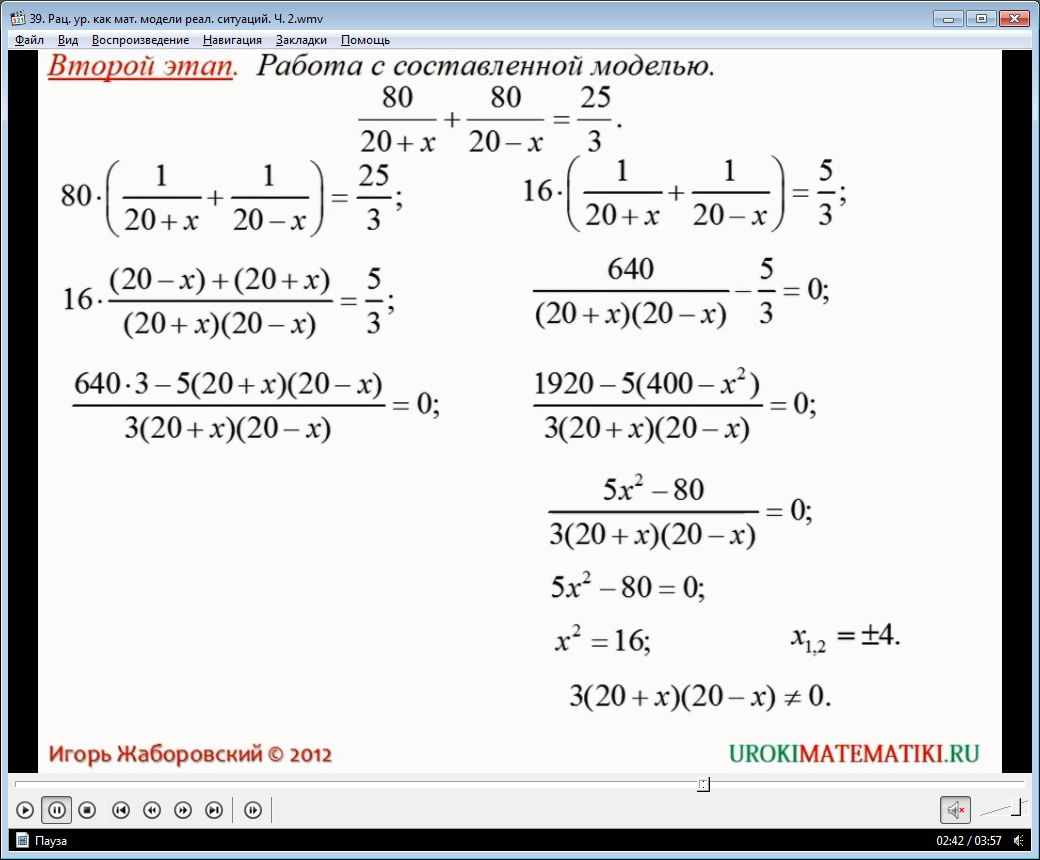
Работа с составленной моделью.
(60/15 + х) + (60/15 - х) = 37/6;
60(1/(15 + х) + 1/(15 - х)) = 37/6.

Выполняем следующие преобразования:
60((15 – х) + (15 + х))/(15 – х)(15 + х)) = 37/6;
1800/((15 + х)(15 – х)) – 37/6 = 0;
(1800*6 – 37(15 + х)(15 – х))/6(15 + х)(15 - х) = 0;
(10800 – 37(225 – х2))/6(15 + х)(15 - х) =0;
(1080 – 8325 – 37х2)/6(15 + х)(15 - х) = 0;
(37х2 - 2475)/6(15 + х)(15 - х) = 0.
Из уравнения 37х2 – 2475 = 0 находим корни. И устанавливаем, удовлетворяют ли они наши условия.
Третий этап решения задачи вы можете проделать по аналогии примера из видеоурока.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 3403 |
| Номер материала | 561 |