
Урок "Рациональные уравнения как математические модели реальных ситуаций" часть 3

Краткое описание документа:
В данном видеоуроке рассматривается тема «Рациональные уравнения как математическую модель реалистичных ситуаций». Тема несложная, однако, лучше рассмотреть ее с репетитором или учителе. Достаточно один раз полностью понять ее, и в дальнейшем не будут возникать проблемы. «Рациональные уравнения как математическую модель реалистичных ситуаций» тесно граничится с различными практическими задачами, с которыми восьмиклассники должны столкнуться. У них сформируется необходимая база навыков, с помощью которых они смогут справляться с различными типами задач, которые можно решить с помощью создания моделей, в основе которых рациональные уравнения.
Справляться с рациональными уравнениями школьники к моменту изучения данной темы должны уметь. Это важный раздел, который охватывает огромное количество различных тем и заданий.
Видеоурок поможет провести достаточно продуктивный и интересный урок для учащихся восьмого класса. Они смогут полноценно освоить и понять данную тему и успешно применять ее на практике.
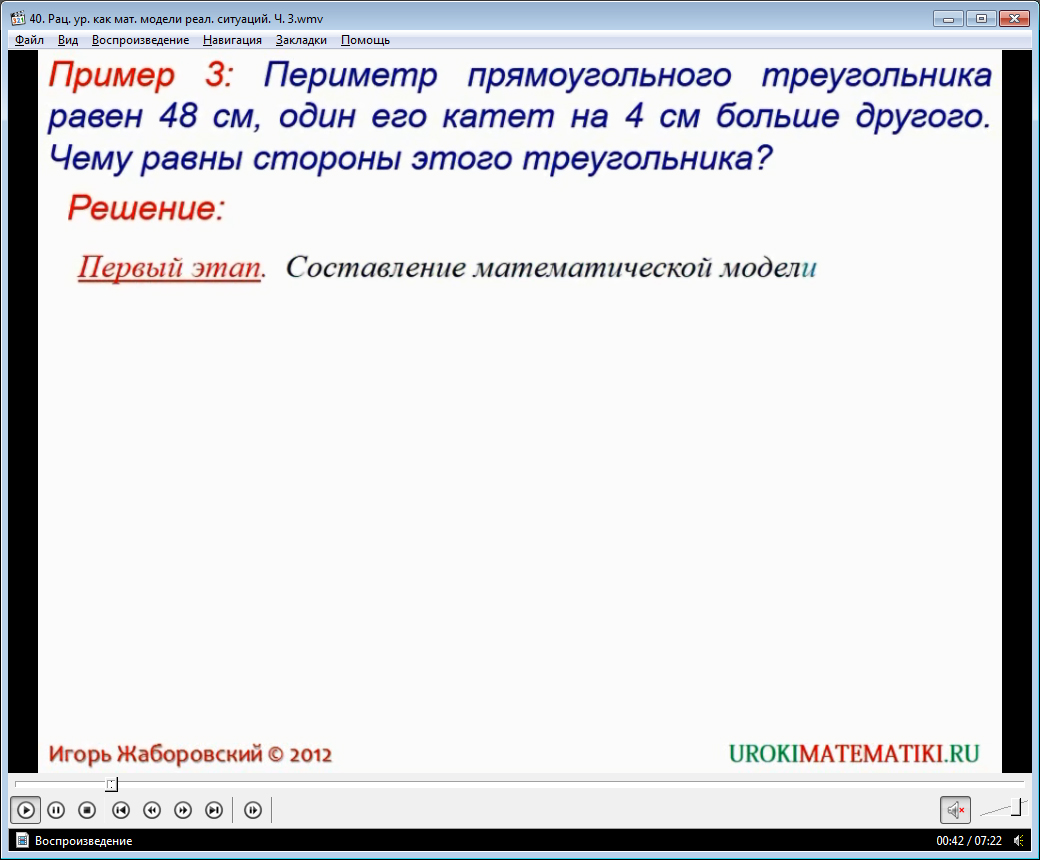
Видеоурок начинается с рассматривания задачи. По сути, она является геометрической. Имеется некоторый треугольник, известен его периметр. Также известно, что некоторый катет треугольник на 4 см больше другого. Ниже приводится подробное решение. Идея заключается в том, что предлагается заменить меньший катет треугольника неизвестным x. Следовательно, можно выразить больший катет, основываясь на известные данные.
Так как мы знаем периметр треугольника, то зная его определения, можно легко записать формулу гипотенузы. Если вычесть из периметра длины катетов, то получим гипотенузу.
Теперь можно записать уравнение, основываясь на теорему Пифагора, которая гласит о том, что сумма квадратов катетов равна сумме гипотенузы.
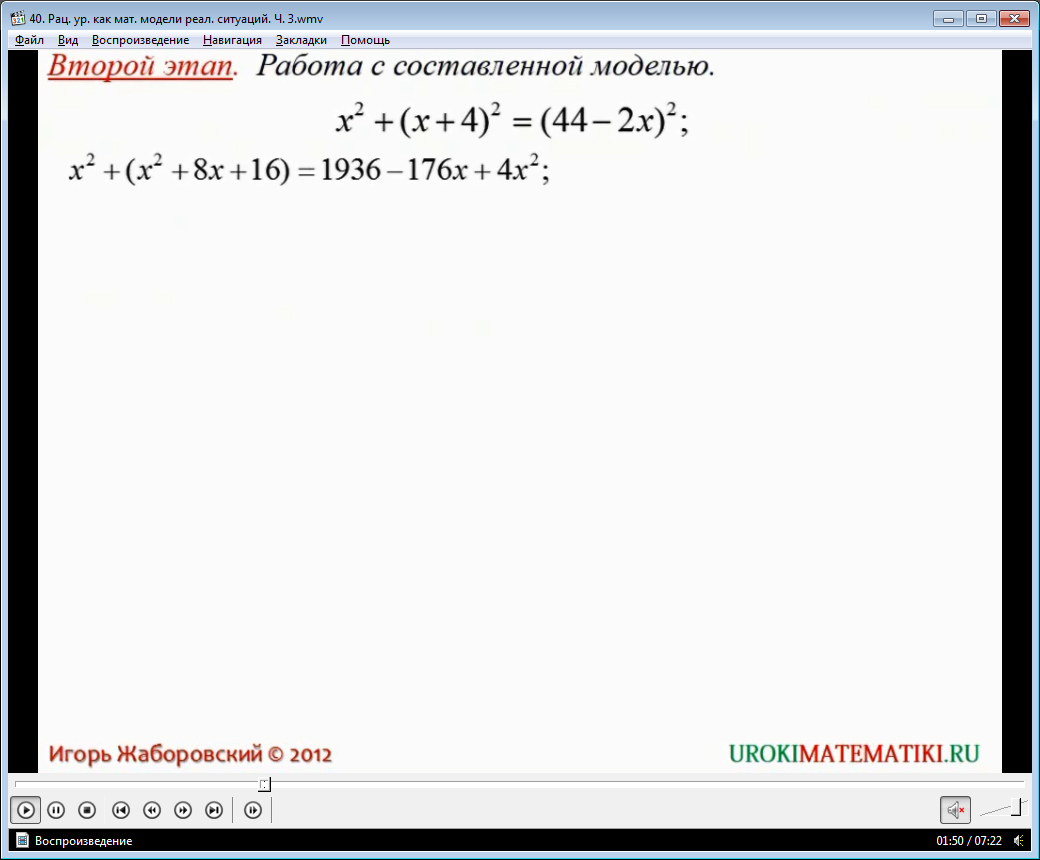
На втором этапе рассматривается полученное уравнение. Приводятся некоторые упрощения для дальнейшей работы с ним. При выполнении этих действий используется формула квадрата суммы, которую необходимо вспомнить.
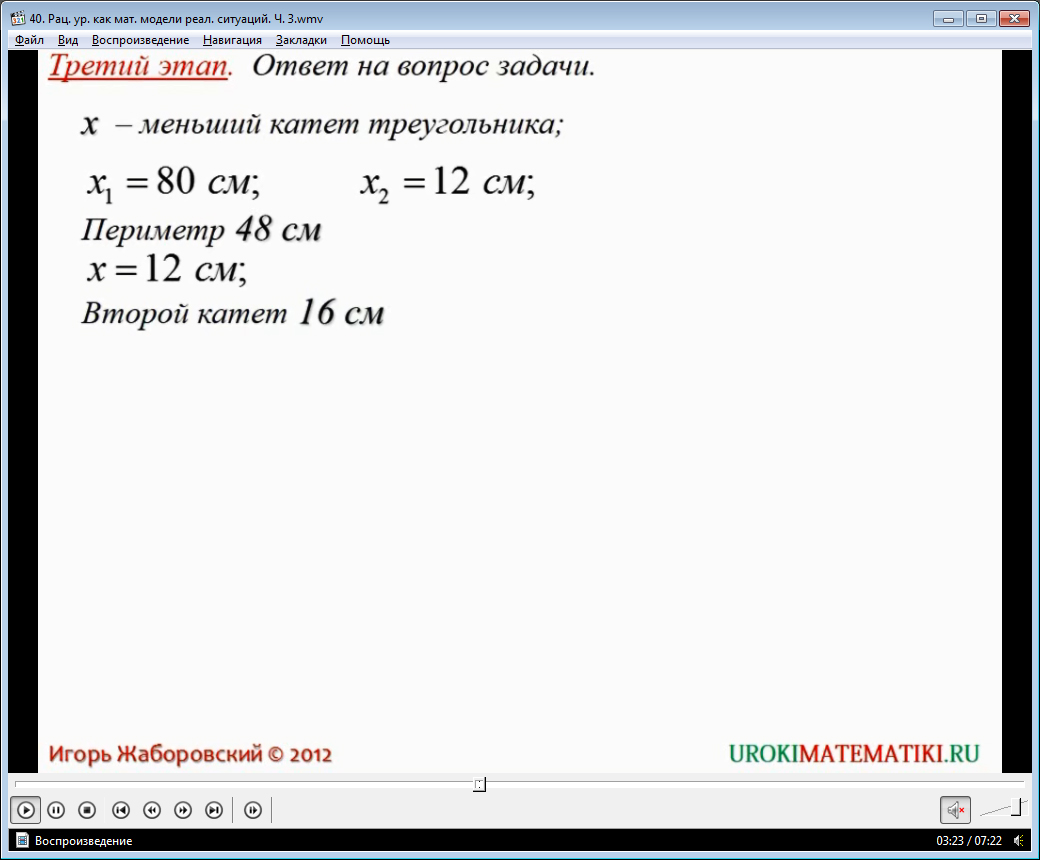
В результате получается два корня, представляющие собой рациональные значения.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 2939 |
| Номер материала | 562 |