
Урок «Объем тел. Понятие объема»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Любое геометрическое тело в пространстве характеризуется объемом. Так что же такое объем пространственной фигуры?
Чтобы найти объем сначала выбирают единицу измерения. Единицей объема в Древнем Риме служила амфора (около 25,5 л).
Нефть во всем мире измеряют в англо-американских единицах - баррелях, то есть в бочках емкостью 159 литров.

Распространённая в России бытовая единица измерения объема — ведро.
За единицу измерения объема в геометрии принимаем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называется кубическим сантиметром, и обозначают . Аналогично определяются кубический метр ( ), кубический миллиметр ( ).
При выбранной единице измерения объем каждого тела выражается положительным числом, которое показывает, сколько единиц измерения объемов и частей единицы содержится в данном теле. Число, выражающее объем тела, зависит от выбора единицы измерения объемов, и поэтому единица измерения объемов указывается после этого числа.
Перечислим свойства объемов:
Свойство 1. Равные тела имеют равные объемы.
Замечание: равенство двух фигур в стереометрии определяется так же, как в планиметрии: два тела называются равными, если их можно совместить наложением.
Например, два параллелепипеда с соответственно равными измерениями, или две пирамиды, у которых соответственно равны стороны оснований и высоты.
Свойство 2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
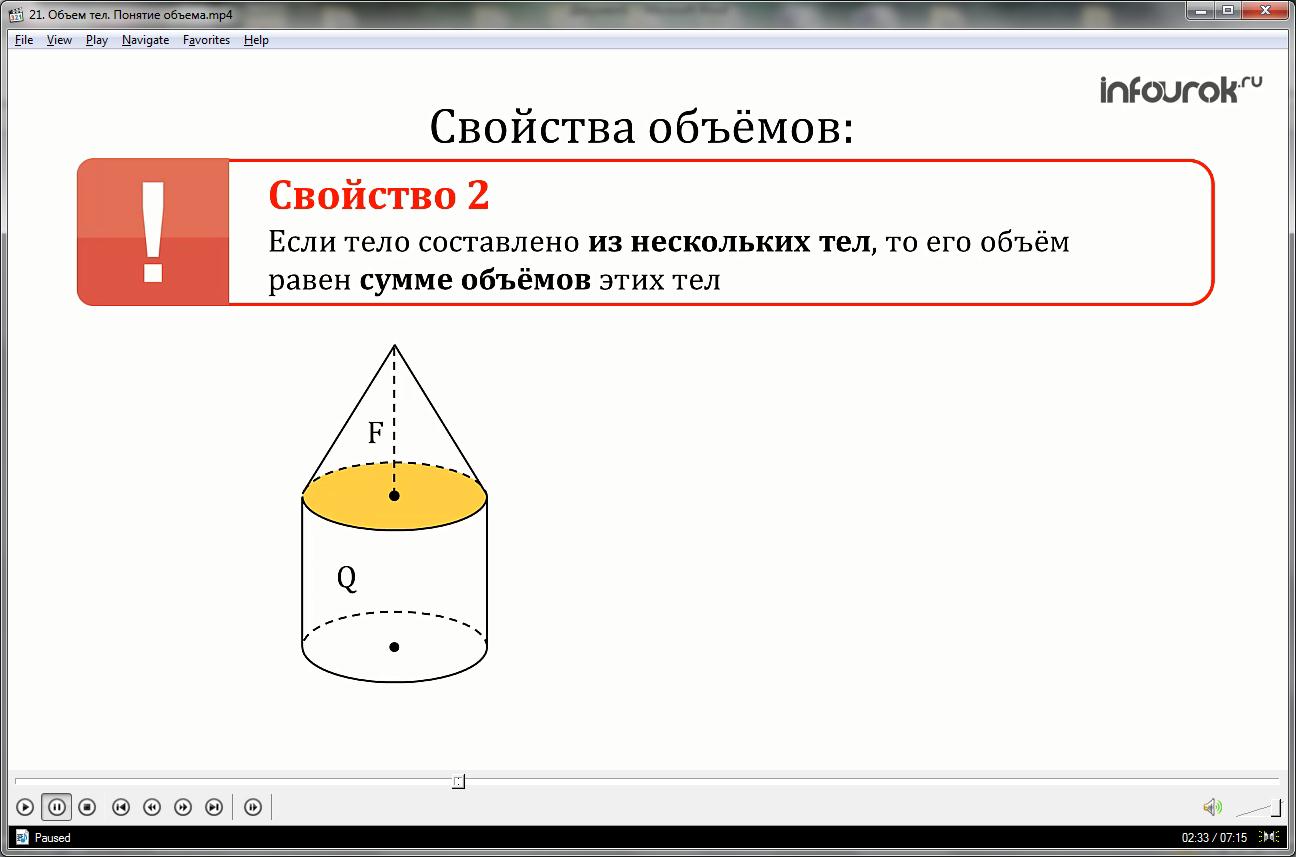
Пусть тело составлено из нескольких тел. При этом мы предлагаем, чтобы любые два из этих тел не имеют общих внутренних точек, но могут иметь общие граничные точки (цилиндр Q и конус F имеют общие граничные точки — точки их общего основания). Объем всего тела складывается из объемов состоящих его тел.
Свойство 3. Если одно тело содержит другое, то объем первого тела не меньше объёма второго.
Допустим, длина ребра куба равна а=1 см, тогда объем куба будем искать по формуле объем куба равен кубу его ребра V= , следовательно, V= , разобьём ребро куба на пять частей , тогда объем куба также будем искать по формуле: объем куба равен кубу его ребра V= , следовательно, равно одной пятой в кубе, возводим дробь в третью степень, получается единица, деленная на 5 в третьей степени или одна сто двадцать пятая сантиментов кубических = .
Получается, что объем тела, содержащегося во втором теле, меньше. Из данного свойства следует:
Следствие: объем куба ребром равен .
Если взять куб, длина ребра которого равна а=1 см, тогда объем куба будем искать по формуле объем куба равен кубу его ребра V= , следовательно, V= и разбить ребро на n частей , тогда объем куба также будем искать по формуле: объем куба равен кубу его ребра V= , следовательно, равно одной энной в кубе, возводим дробь в степень, получается единица деленная на n в третьей степени = . Следствие доказано.

Задача 1.
Найдите объём многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Решение: Пусть измерения синего параллелепипеда: =4
По формуле нахождения объема прямоугольного параллелепипеда умножаем длину на ширину и на высоту синего прямоугольного параллелепипеда: = . Подставляем в формулу значения и считаем:
По чертежу находим измерения зеленого прямоугольного параллелепипеда:
По формуле нахождения объема прямоугольного параллелепипеда умножаем длину на ширину и на высоту зеленого прямоугольного параллелепипеда: = .
Подставляем в формулу значения и считаем:
По свойству второму, чтобы найти объем тела, нужно сложить объемы двух тел (зеленого и синего прямоугольных параллелепипедов), из которых оно состоит V= . Подставляем значения в формулу и считаем: V=
Ответ: объем фигуры равен 39.
Задача 2.
Размер кирпича 250x120x65. Необходимо заложить проем в стене размером 2200х120х700. Сколько кирпичей необходимо приобрести для выполнения ремонта?

Решение:
Сначала найдем объем одного кирпича (пусть - это длина кирпича, - ширина кирпича, -высота кирпича; -длина проема, -ширина проема, -высота проема.
Тогда объем одного кирпича обозначим и он будет равен
-длина проема, -ширина проема, -высота проема.
Найдем — объем проема в стене
Чтобы найти количество кирпичей нужно объем стенного проема разделить на объем одного кирпича:
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9752 |
| Номер материала | 1007 |