
Урок "Сложение и вычитание алгебраических дробей с одинаковыми знаменателями"

Краткое описание документа:
Сложение и вычитание математических дробей с одинаковыми знаменателями является базовой операцией во многих случаях. Например, все более сложные выражения, включающие дроби с разным типом знаменателя, в процессе решения всегда сводятся к более простым вариантам – знаменатель стараются обобщить. Как только выражение из дробей приводится к многочлену, имеющему общий знаменатель, оно может быть развязано довольно легко и быстро.
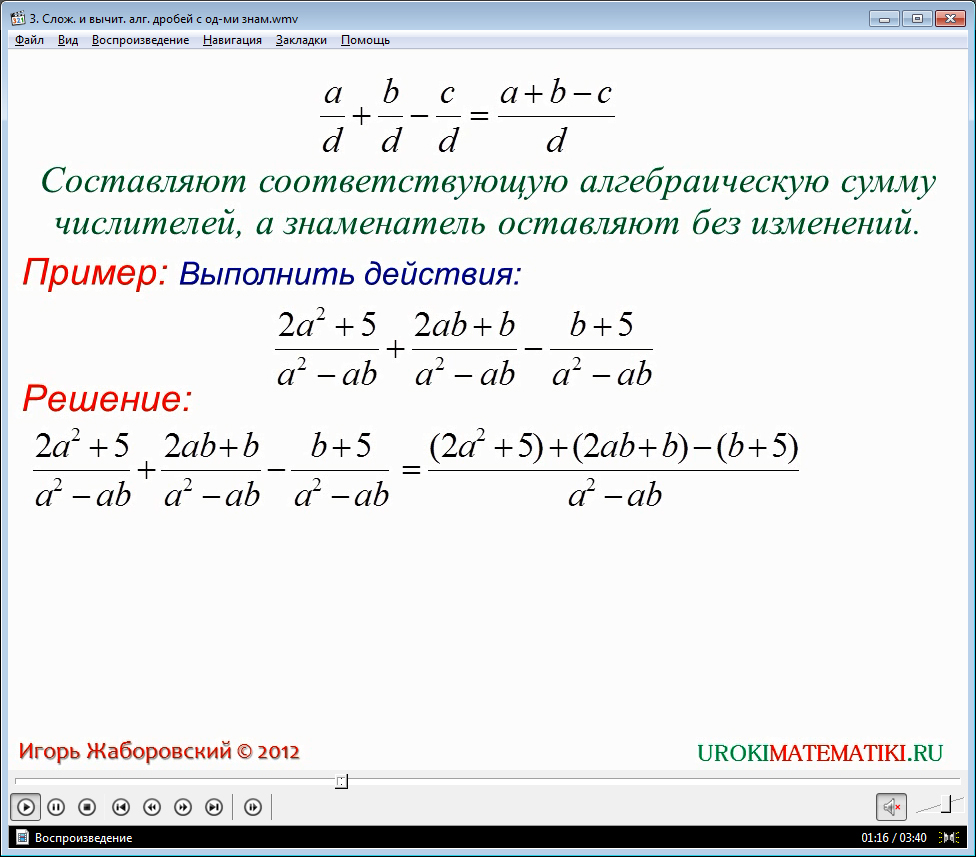
В представляемом видео прекрасно иллюстрирован первоначальный общий подход к решению выражений из дробей с одинаковыми знаменателями. Необходимо сразу сделать ремарку, что если многочлен содержит какие-либо элементы, имеющие отличный от общего знаменатель, то его можно решить лишь частично.
Чтобы понимать механизм решения подобных уравнений, следует провести более открытый анализ происходящего процесса. В данном случае, все элементы многочлена, имеющие общий знаменатель, делятся на некоторый коэффициент, который выносится за скобки. Этот коэффициент должен быть равен единице, деленной на значение знаменателя:
a/d + b/d + c/d = 1/d(a+b+c)
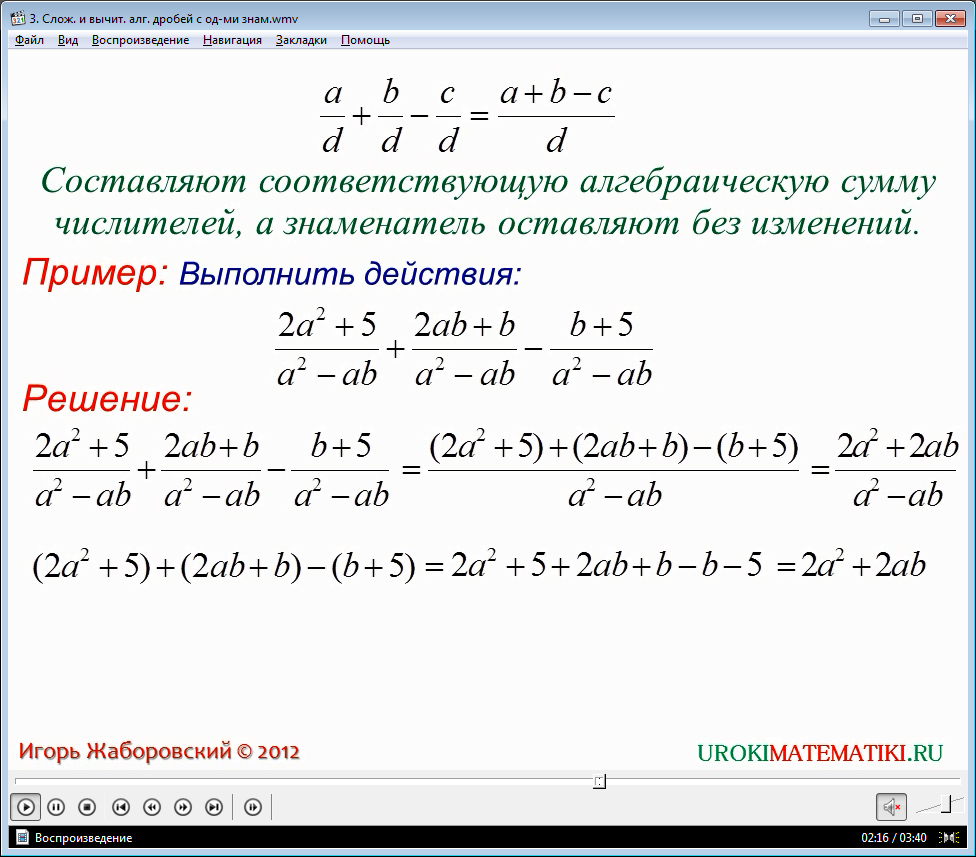
Как показано в видеоуроке, после совершения этой процедуры, необходимо провести обычное алгебраическое сложение получившегося в скобках выражения. При этом знаки при числах сохраняются неизменными – в зависимости от того, какими они были в первоначальном многочлене.
Пример 1. Развязать выражение -5/16 + 4/16 – 3/16
Как мы видим, общий знаменатель тут один, и равен он 16. Выбираем коэффициент, равный 1/16, и поочередно делим каждый элемент на данный коэффициент. В результате, получаем выражение, довольно легко решающееся элементарным алгебраическим сложением и последующим произведением вынесенного коэффициента на получившуюся сумму многочлена в скобках:
-5/16 + 4/16 – 3/16 = 1/16(-5 + 4 - 3) = 1/16(-4) = -(4/16)
Главное при решении подобных задач - не упустить знак перед числовым значением. Знание основ алгебраического сложения дробей с одинаковыми знаменателями может помочь довольно легко решить весьма мудреные, на первый взгляд, выражения, представленные в видеоуроке.
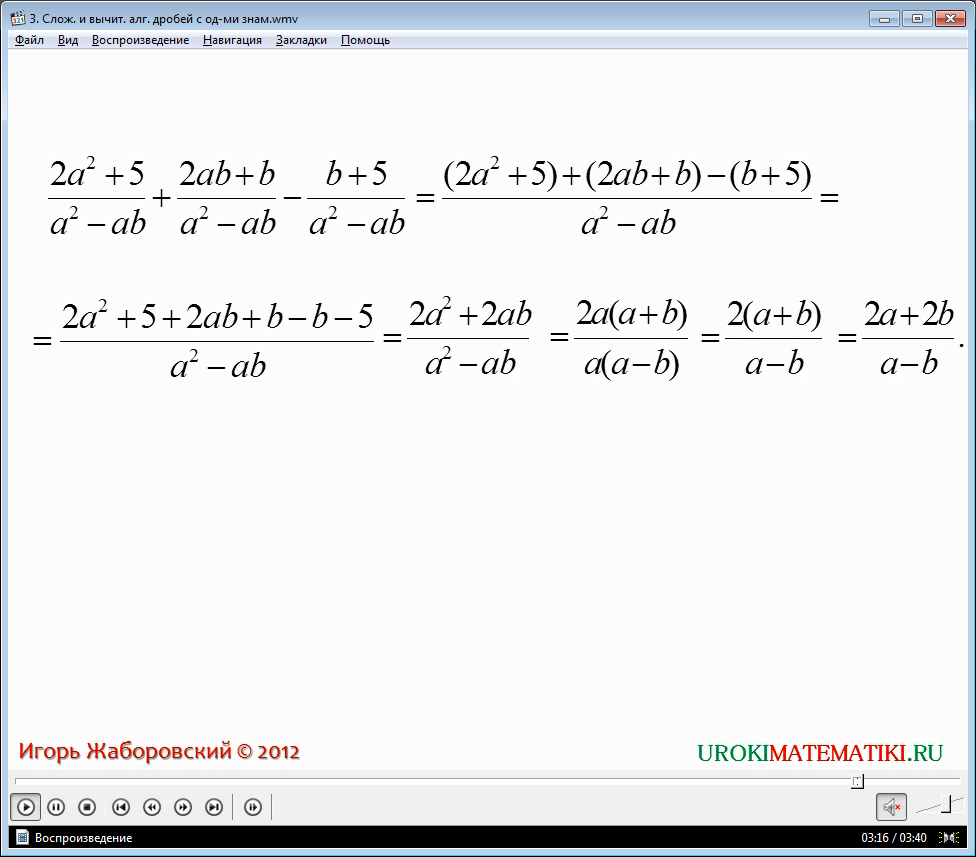
Пример 2. Развязать выражение (3a – 7b)/m + (-3a + 4c)/m – (2c – 2b)/m
Имеем общий знаменатель m, выносим в качестве коэффициента значение 1/m за скобки всего выражения:
(3a – 7b)/m + (-3a + 4c)/m – (2c – 2b)/m =
= 1/m(3a – 7b + (-3a) + 4c – (2c – 2b)) =
= 1/m(3a – 7b – 3a + 4c – 2c + 2b) =
= 1/m(-5b + 2c) = -(5b -2c)/m
В подобных случаях, помним правило, что если перед скобкой стоит знак минус, то все знаки внутри меняются на противоположные.
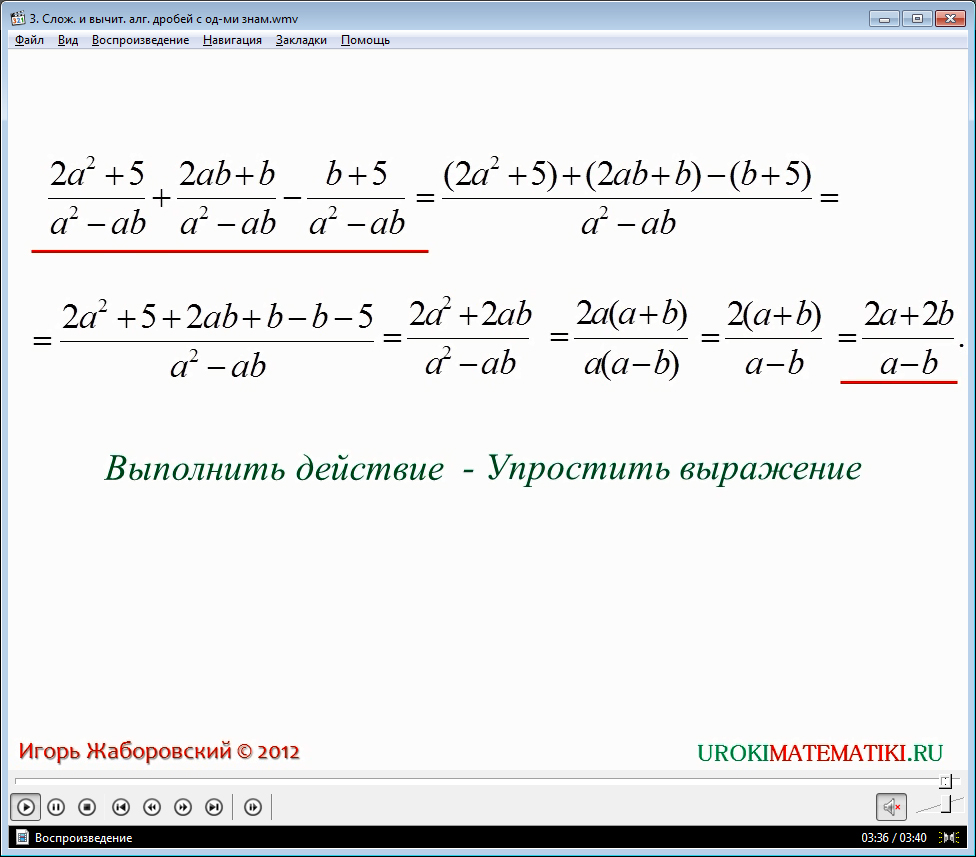
Таким образом, для решения уравнений представленного вида можно создать следующий алгоритм:
1. Группируем (при необходимости) все элементы, имеющие единый знаменатель – в дальнейшем, все операции будут проводиться строго над этой группой.
2. Коэффициент, равный 1/общий знаменатель выносим за скобки.
3. Алгебраически суммируем выражение в скобках, не забывая элементарные правила по совмещению разных знаков.
4. Умножаем коэффициент на полученное в скобках значение.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5453 |
| Номер материала | 526 |