
Урок "Выражения с переменными"

Краткое описание документа:
Решение задач и некоторых выражений не всегда приводит к чистым числовым ответам. Даже в случае тривиальных расчетов, можно прийти к определенной конструкции, именуемой выражением с переменной.
Например, рассмотрим две практические задачи. В первом случае у нас есть некий завод, вырабатывающий 5 тонн молока каждый день. Необходимо найти, сколько молока вырабатывается заводом за р дней.
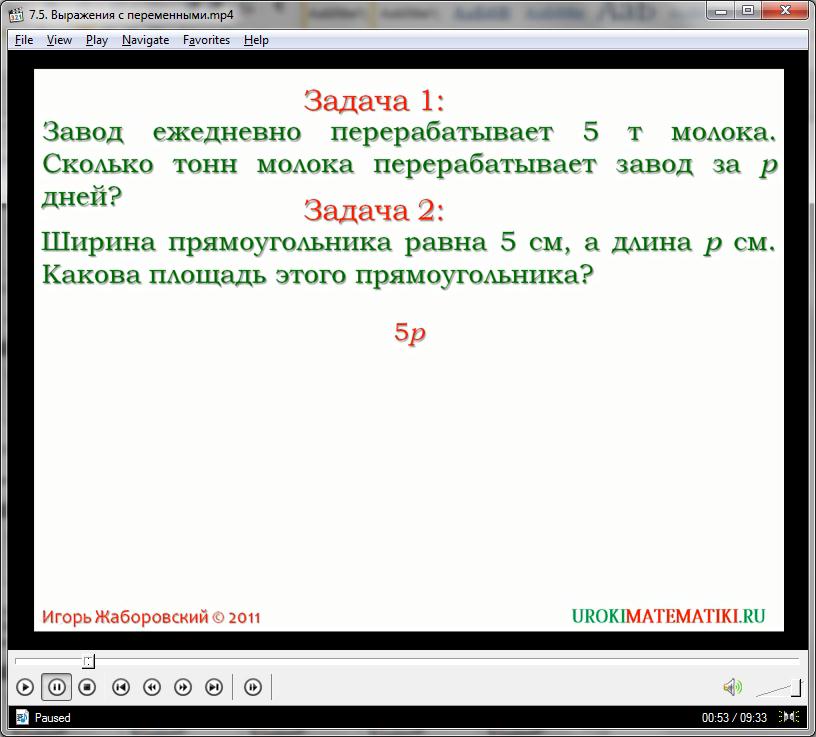
Во втором случае есть прямоугольник, ширина которого равна 5 см, а длина р см. Найти площадь фигуры.
Разумеется, если завод вырабатывает пять тонн в день, то за р дней, по простейшей математической логике, он выдаст 5р тонн молока. С другой стороны, площадь прямоугольника равна произведению его сторон – то есть, в данном случае, это 5р. Иными словами, в двух тривиальных задачах с разными условиями, ответом является одно целое выражение – 5р. Подобные одночлены именуются выражением с переменной, так как помимо числовой части они содержат некоторую букву, именуемую неизвестной, или переменной. Обозначается такой элемент строчными буквами латинского алфавита, чаще всего, х или у, хотя это не принципиально.
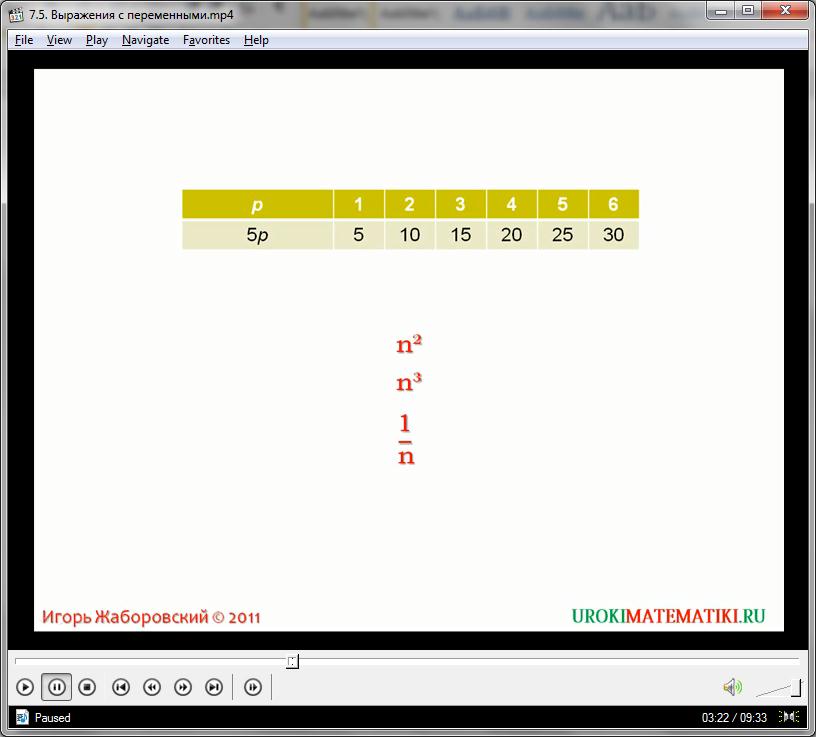
Особенностью переменной является то, что она может принимать любые значения на практике. Подставляя разные числа, мы будем получать итоговое решение для наших задач, например, для первой:
р = 2 дня, завод выдает 5р = 10 тонн молока;
р = 4 дня, завод выдает 5р = 20 тонн молока;
Или для второй:
р = 10 см, площадь фигуры равна 5р = 50 см2
р = 20 см, площадь фигуры равна 5р = 100 см2
Важно понимать, что р – это не набор некоторых отдельных значений, а все множество, которое будет математически соответствовать условию задачи. Основная роль переменной – это заменить недостающий элемент в условии. Любая математическая задача должна включать некоторые конструкции и отображать взаимосвязь между этими конструкциями в условии. Если значения какого-либо объекта не хватает, то вместо него и вводится переменная. При этом она является абстрактной заменой именно самого элемента условия (количества чего-либо, представленного числом, или выражением), а не функциональных связей.
Если рассматривать выражение вида 5р, как нейтральный и независимый объект, то значение р в нем может принимать какие угодно значения, фактически р тут равен множеству всех действительных чисел.
Но в наших задачах на ответ в виде 5р накладываются определенные математические ограничения, которые вытекают из условий. Например, дни и сутки не могут быть отрицательными, поэтому р в обеих задачах всегда равен нулю или больше его. Кроме того, дни не могут быть дробными – для первой задачи действительны только те значения р, которые являются целыми положительными числами.
В первой задаче: р равно конечному множеству всех положительных целых чисел;
Во второй задаче: р равно конечному множеству всех положительных чисел.
Выражения могут включать и сразу две переменные, например:
2х + 3у
В данном случае, бином представлен двумя одночленами, каждый из которых имеет переменную в составе, причем эти переменные являются разными, то есть – независимыми друг от друга. Значение этого выражения может быть рассчитано полностью только при наличии значения обеих переменных. Например, если х = 2, а у = 4, то:
2х + 3у = 4 + 12 = 16 (при х = 2, у = 4)
Стоит отметить, что в этом выражении нет математических, или логических ограничений на значения переменной – и х, и у принадлежат всему множеству действительных чисел.
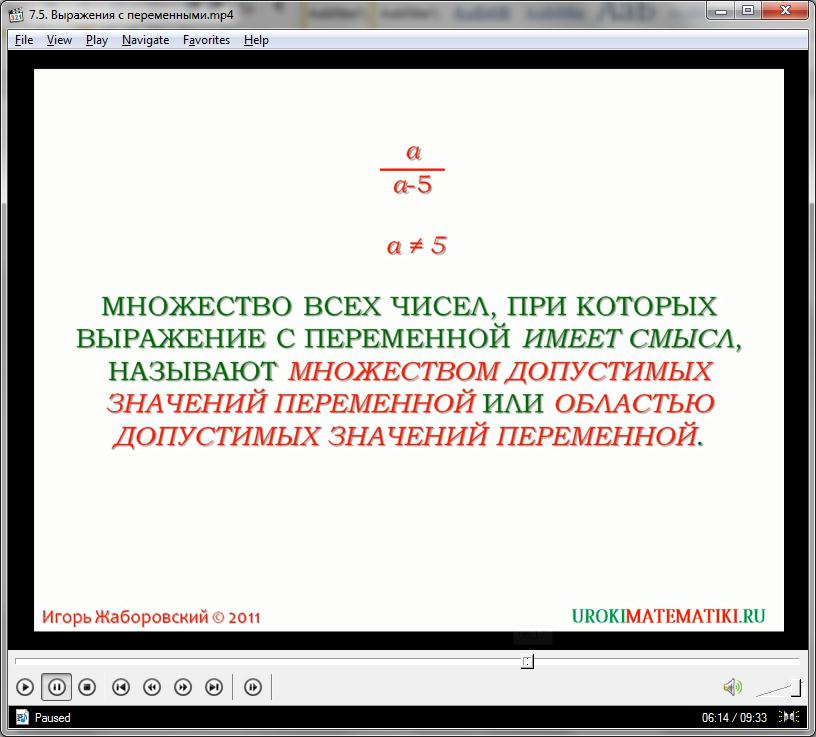
В общем плане, множество всех чисел, при подстановке которых вместо переменной выражение сохраняет смысл и действительность, называется областью определения (или значения) переменной.
В абстрактных примерах, не связанных с реальными задачами, область определения переменной чаще всего либо равна всему множеству действительных чисел либо ограничивается некоторыми конструкциями, например, дробью. Как известно, при нулевом значении делителя вся дробь теряет смысл. Поэтому переменная в выражении вида:
7х/(х – 5)
не может быть равна пяти, так как тогда:
7х/(х – 5) = 7х/0 (при х = 5)
И дробь потеряет смысл. Поэтому для этого выражения переменная х имеет область определения – множество всех чисел за исключением 5.
В нашем видеоуроке отмечен также особый случай применения переменных, когда они обозначают число одного порядка. Например, числа 54, 30, 78 можно задать через переменную а, либо же через конструкцию аb (с горизонтальной чертой сверху, для отличия от произведения), где b задает единицы (соответственно 4, 0, 8), а – десятки (соответственно, 5, 3, 7).
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6367 |
| Номер материала | 444 |