
Урок "Приведение дробей к общему знаменателю"

Краткое описание документа:
На протяжении изучения курса математики в тех или иных задачах школьники будут сталкиваться с необходимостью проведения разных операций над дробями, где числители и знаменатели могут представлять собой как обычные числовые выражения, так и сложные степенные буквенные выражения.
Для начала нужно уметь приводить простые численные дроби к общему знаменателю, а после переходить к более сложным выражениям.
С помощью видеоурока «Приведение дробей к общему знаменателю» можно объяснить школьнику соответствующего класса, как правильно проводить данную операцию. Электронный обучающий ресурс начинается с того, что диктор рассказывает, как можно простую дробь привести к знаменателю с другим значением. Чтобы это понять, необходимо вспомнить основное свойство дроби, гласящее, что числитель и знаменатель любой дроби можно умножить на одно и то же число и, тем самым, ее значение не измениться. Опираясь на это, в видеоуроке дробь 3/4 приводится к иной дроби, равной изначальной, со знаменателем 8. Для этого и числитель, и знаменатель умножается на натуральное число 2.
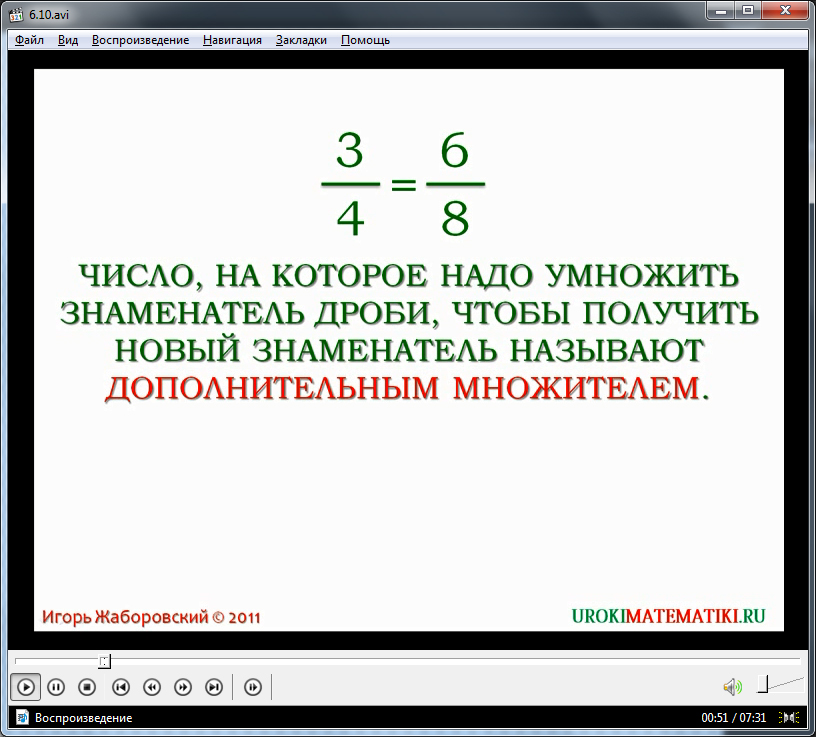
Далее на экран выводится определение понятия дополнительный множитель. В предыдущем примере дополнительным множителем является 2. Основное понятие в определении выделяется красным цветом, чтобы школьник мог сконцентрировать свое внимание на нем, тем самым запоминая определение в целом.
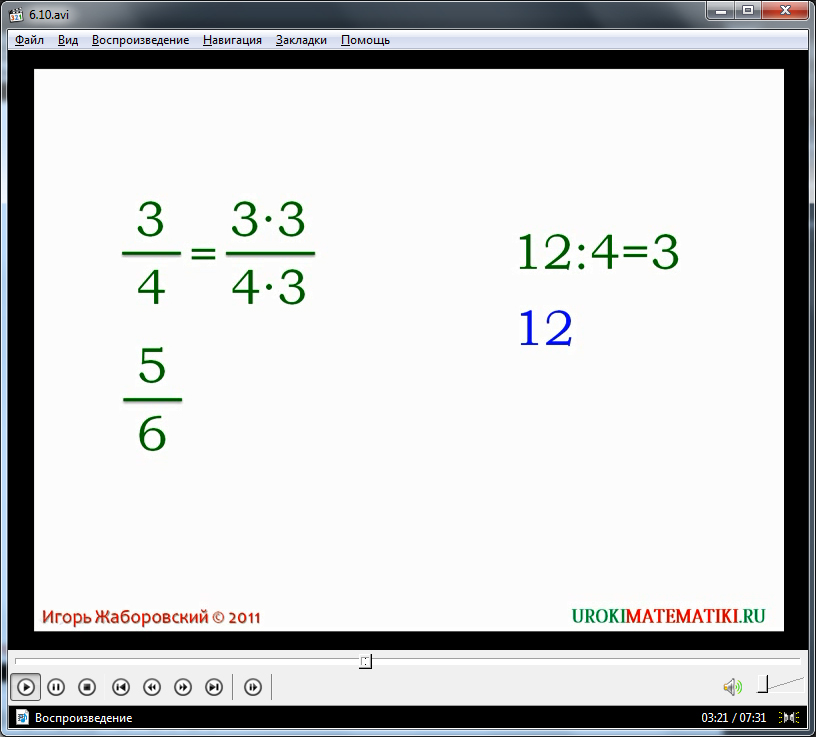
Если необходимо привести дробь к определенному значению, то нетрудно догадаться, что необходимо поделить на данное число знаменатель. Тем самым можно найти дополнительный множитель. Данная операция демонстрируется в видеоуроке и комментируется диктором на примере дроби 2/7. После нахождения дополнительного множителя на него умножается и числитель и знаменатель дроби. Получаем искомый результат.
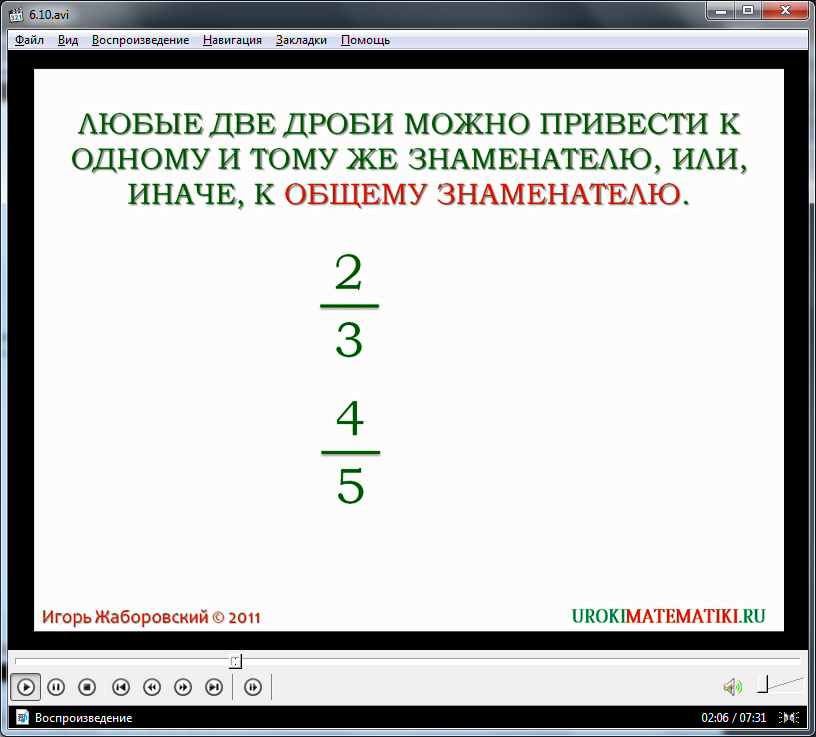
Эту операцию можно провести абсолютно с любыми дробями. Она называется приведением дроби к общему знаменателю. Его определение можно предложить школьникам записать в тетради.
Для того чтобы найти наименьший общий знаменатель, необходимо вспомнить процедуру нахождения наименьшего общего кратного, то есть такое наименьшее число, которое делится и на первый знаменатель, и на второй рассматриваемых дробей.
Как видим, ничего сложного в данной операции нет. Необходимо понять и запомнить несложную цепочку действий, которую можно закрепить на практических примерах. Их можно взять непосредственно из видеоурока.
Пошаговый алгоритм демонстрируется подробным образом и на примере практики и в виде текста. Для развития математической речи можно предложить ученику самостоятельно рассказать алгоритм при решении примера.
В завершающей части электронного урока демонстрируется практический пример приведения дробей к общему знаменателю, при котором подробно выполняется и поиск наименьшего общего кратного.
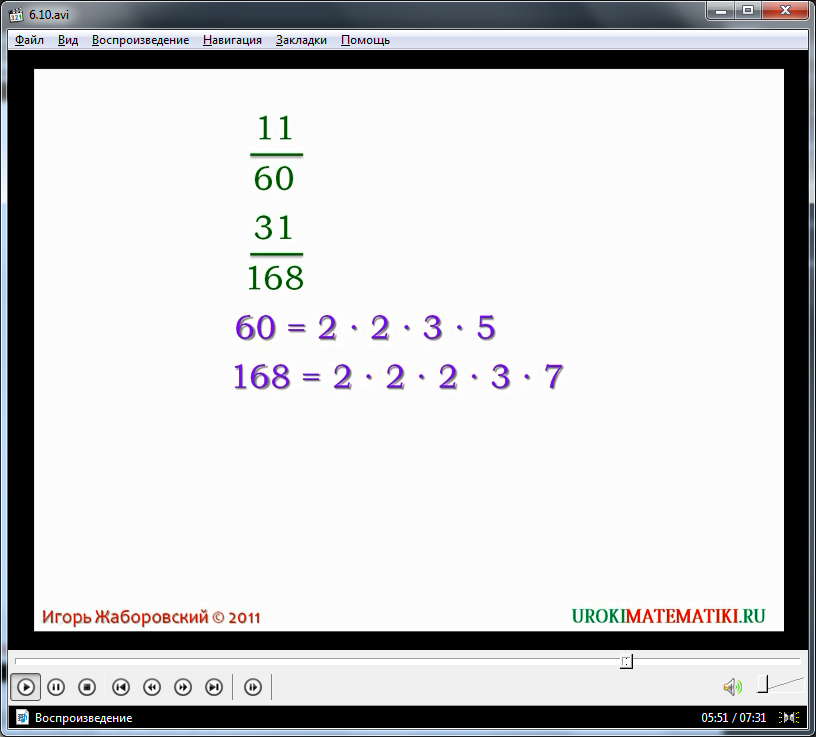
Операция проводится над дробями 11/60 и 31/168. На первом этапе, согласно начальному пункту ранее изложенного алгоритма, необходимо найти наименьшее общее кратное знаменателей – 60 и 168. Для этого, если вспомнить предыдущие уроки, необходимо разложить данные натуральные числа на простые множители. Выбирая необходимые множители (как это сделать, рассказывается в уроке «Наименьшее общее кратное») получаем искомое число, которое и является наименьшим общим знаменателем. Далее находится дополнительный множитель, о котором шла речь ранее. Умножая числитель и знаменатель на это число, диктор сообщает о полученном искомом результат – 154/840.
Данный видеоурок будет полезным школьникам, обучающимся на дому, репетиторам, родителям и учителям. Также ученики могут подготовиться к грядущему уроку самостоятельно, развить свои навыки и увеличить знания.
Текст, используемый в данном ресурсе, будет понятным для учеников 6 класса. Он не содержит в себе сложных оборотов и непонятных определений.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 7370 |
| Номер материала | 432 |