
Урок "Сокращение дробей"

Краткое описание документа:
Сокращение дробей тесно связано с основным их свойством. Эта тема очень важна в курсе изучения алгебры во всех школах, независимо от направления. Уметь правильно сокращать дроби должен каждый ученик, начиная с 6 класса. С помощью этого большие дробные выражения могут быть сокращены до минимума, тем самым работа с ними во многом упроститься и не займет большого количества времени.
Теме «Сокращение дробей» посвящена данная видеозапись. Некоторые другие обучающие ресурсы также относятся к данной области. Они все тесно взаимосвязаны, поэтому необходимо изучить их всех должным образом без пропусков. Не умея правильно сокращать дроби, у учеников возникнут проблемы и при сложении, умножении дробей, делении и других операций с обычными натуральными числителями и знаменателями, а упрощение дробных выражений в неравенствах или уравнениях станет непосильной задачей, что нельзя допустить.
Избегать работе с дробями школьники не смогут не только в алгебре, но и в геометрии и, даже в задачах по физике и химии. Начинать нужно с объяснения элементарной и основной операции – сокращение дробей.
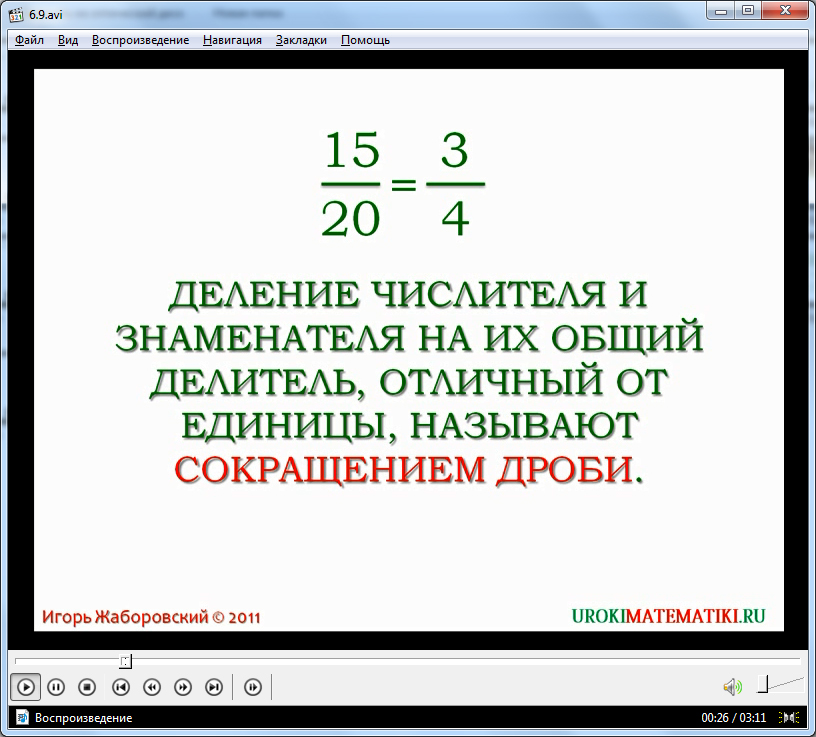
Видеозапись, посвященная данной теме, начинается с демонстрации сокращения дроби, числителем которого является натуральное число 15, а знаменателем – 20. Чтобы провести операцию сокращения, необходимо поделить и числитель, и знаменатель на число 5. Таким образом, диктор сообщает, что в результате получается дробь с числителем, равным 3, и знаменателем, соответственно, 5.
Стоит отметить, что полученная дробь указывает на число, равное изначально заданной дроби, над которой провели операцию сокращения, согласно основному свойству дробей. Чтобы его повторить, можно вернуться к предыдущему обучающему видеоуроку и пересмотреть его.
Каким же образом необходимо сократить дробь? Как видим из предыдущего примера, число 5 является наибольшим общим делителем чисел 15 и 20. Разумеется, школьник должен быть заранее ознакомлен с данным понятием. Рекомендуется, прежде чем начать данную тему, вспомнить необходимые определения из предыдущих уроков.
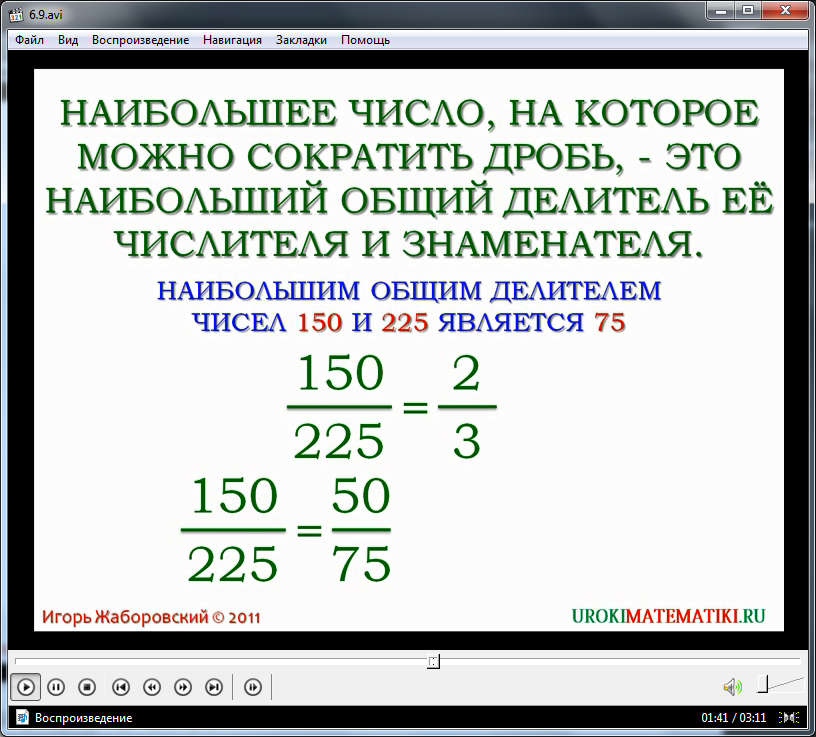
Таким образом, для того, чтобы максимально сократить дробь, необходимо поделить и числитель, и знаменатель на наибольший общий делитель. В результате получим дробь, равную предыдущей, но в сокращенном варианте.
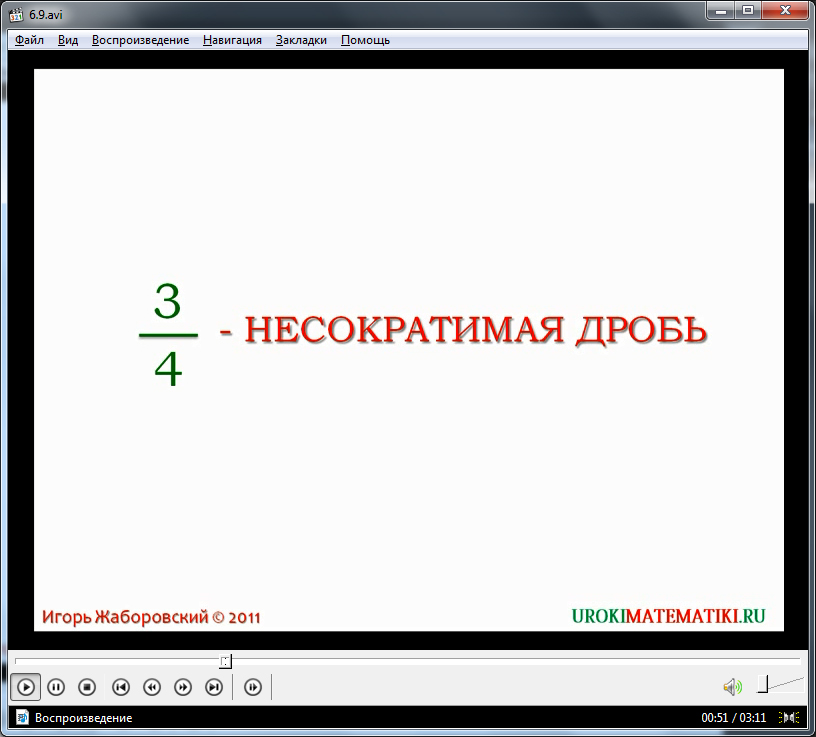
Если числитель и знаменатель некоторой дроби являются взаимно простыми, то ее нельзя сократить. Проверить это можно достаточно просто, что и предлагает диктор в видеоуроке. На экран выводится несократимая дробь 2/3. Натуральные числа 2 и 3 не имеют наибольшего общего делителя, отличного от единицы. Следовательно, они являются взаимно простыми.
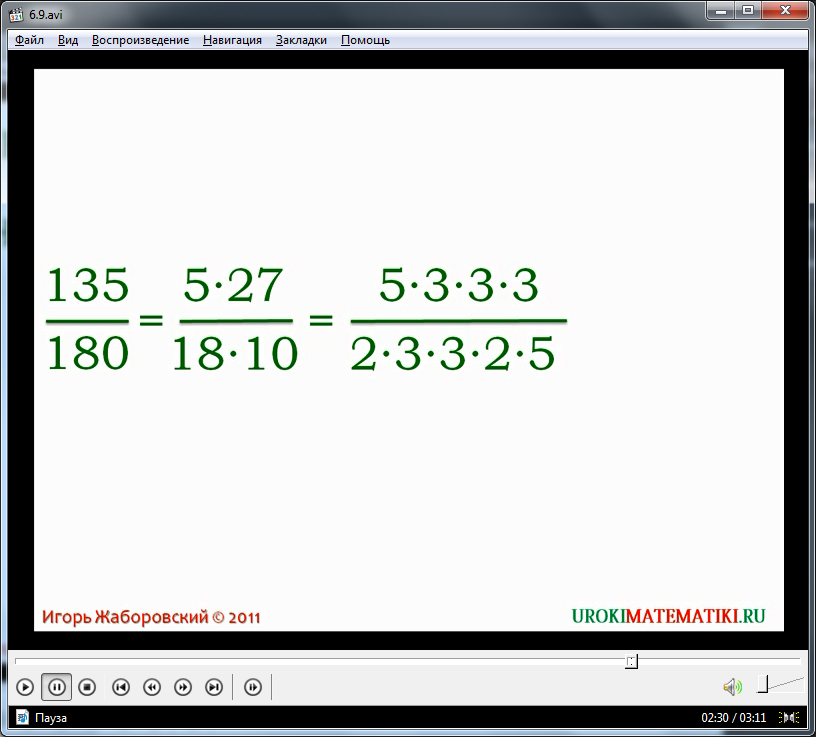
В последней части видеоурока приводится несколько вариантов сокращения дробей, чтобы ученик, просматривающий его, мог как можно лучше понять суть темы. По окончанию урока, необходимо дать учащемуся или учащимся несколько примеров для самостоятельного решения. Если он (они) легко и без подсказок справится с этим, то смело можно перейти к дальнейшему изучению темы «Дроби».
Также, можно проверить теоретические знания школьника – предложить ему ответить на вопросы, которые показаны на экране в конце видеоресурса.
Данный учебный материал будет полезен не только школьникам для домашнего обучения, но и учителям, репетиторам и родителям, которые помогают детям при выполнении домашних заданий, самостоятельно следят за уровнем их знаний.
Материал урока является понятно изложенным и поможет детям, которые не успевают достаточно быстро осваивать тему во время урока в школе, тем самым отставая от своих ровесников.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 8017 |
| Номер материала | 433 |