
Урок «Решение задач на построение сечений»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Подумайте, какой школьный предмет позволяют научиться правильно выполнять и оформлять чертежи, познакомится с различными графи¬ческими способами передачи сведений об объектах предметного мира.
Правильно! Это черчение.
Для изготовления деталей на заводе используются точные чертежи этих деталей в разрезе.
Разрезы используются для показа внутренней формы изделия.
Разрезом называется изображение, полученное при мысленном рассечении детали одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости.
При решении геометрических задач связанных с тетраэдром и параллелепипедом тоже иногда необходимо построить разрез фигуры. Только полученное изображение в геометрии называется сечением.
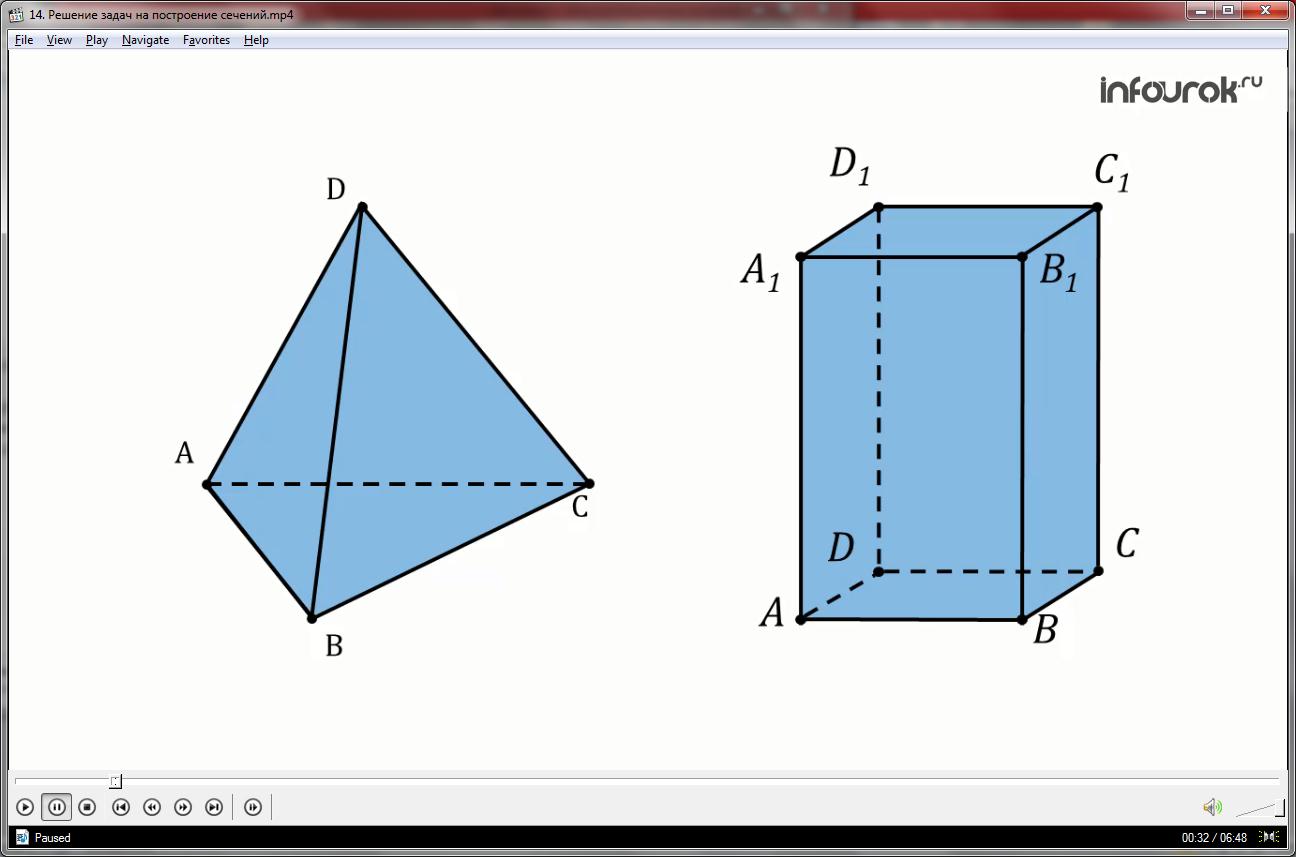
Давайте разберёмся, что называется сечением тетраэдра и параллелепипеда.
Секущая плоскость α пересекает грани тетраэдра по отрезкам АЕ, ЕС, АС. Треугольник АЕС, сторонами которого являются эти отрезки, называется сечением тетраэдра.
Тетраэдр имеет четыре грани, значит его сечениями могут быть только треугольники и четырехугольник.
При пересечении параллелепипеда секущая плоскость также оставляет следы на его боковых гранях в виде отрезков. Отрезки образуют многоугольник, который называется сечением параллелепипеда.
Так как у параллелепипеда шесть граней, то в сечении может получиться фигура треугольник,
на рисунке вы это видите. Четырехугольник
Пятиугольник и шестиугольник .
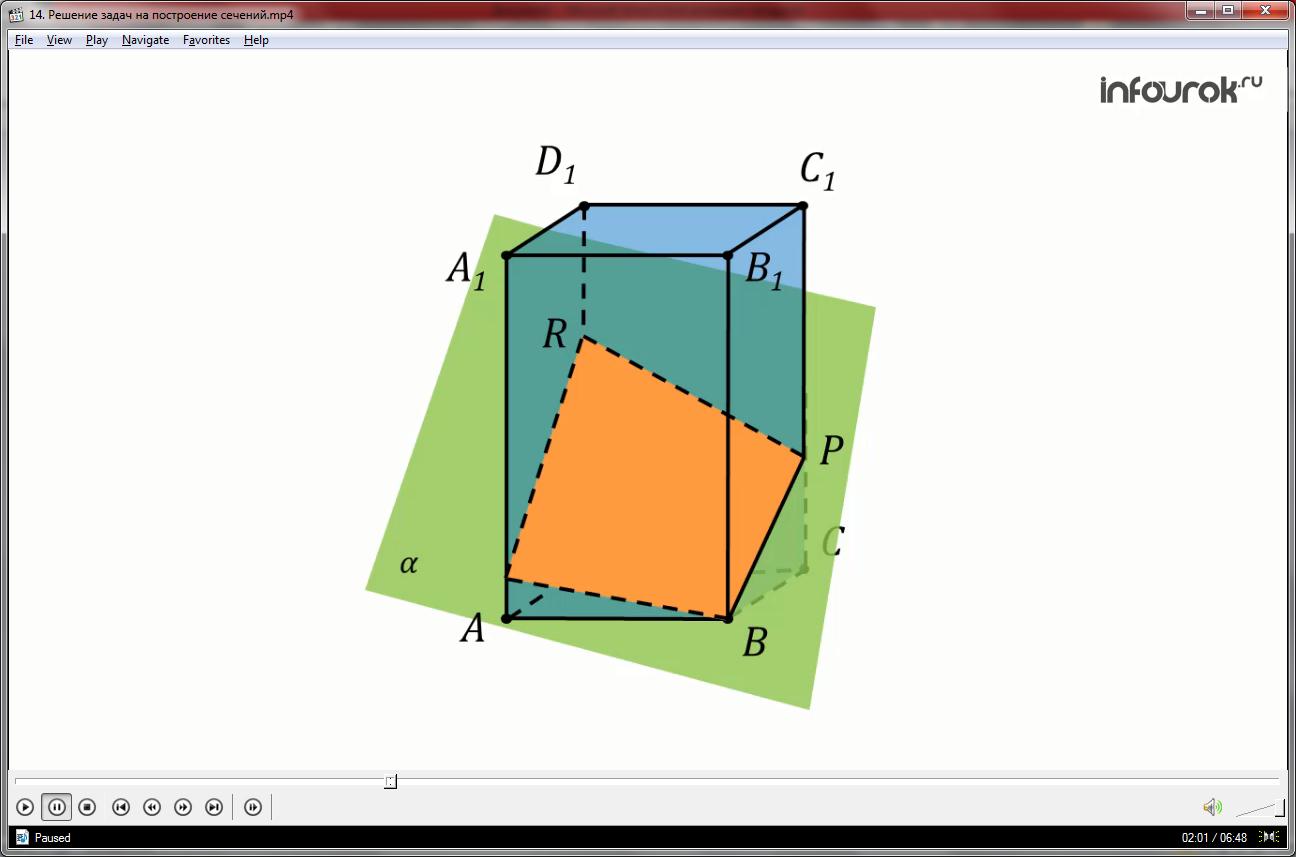
При построении сечений очень легко нарушить геометрические факты, теоремы. Например, данное сечение параллелепипеда плоскостью содержит ошибку.
Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны. Значит, отрезок АВ и отрезок RP на чертеже должны быть изображены параллельно. А мы наблюдаем, что это не так . Но и отрезки AR и BP тоже не параллельны, хотя лежат в параллельных плоскостях. Значит плоскость α, должна пересекать грани АА1D1D и BB1C1C по параллельным прямым.
Исправим ошибки.
Или на данном чертеже прямая LM пересекает ребро ВC в точке N. Но это невозможно. Прямая LM принадлежит плоскости АА1D1D, а прямая ВС не лежит в данной плоскости, значит они не могут пересекаться, они скрещивающиеся прямые. Так прямая LM не может пересекать DC, ВВ1 , а вот c прямой AD они пересекаются.
Исправим ошибку на чертеже.
Рассмотрим примеры построения различных сечений.
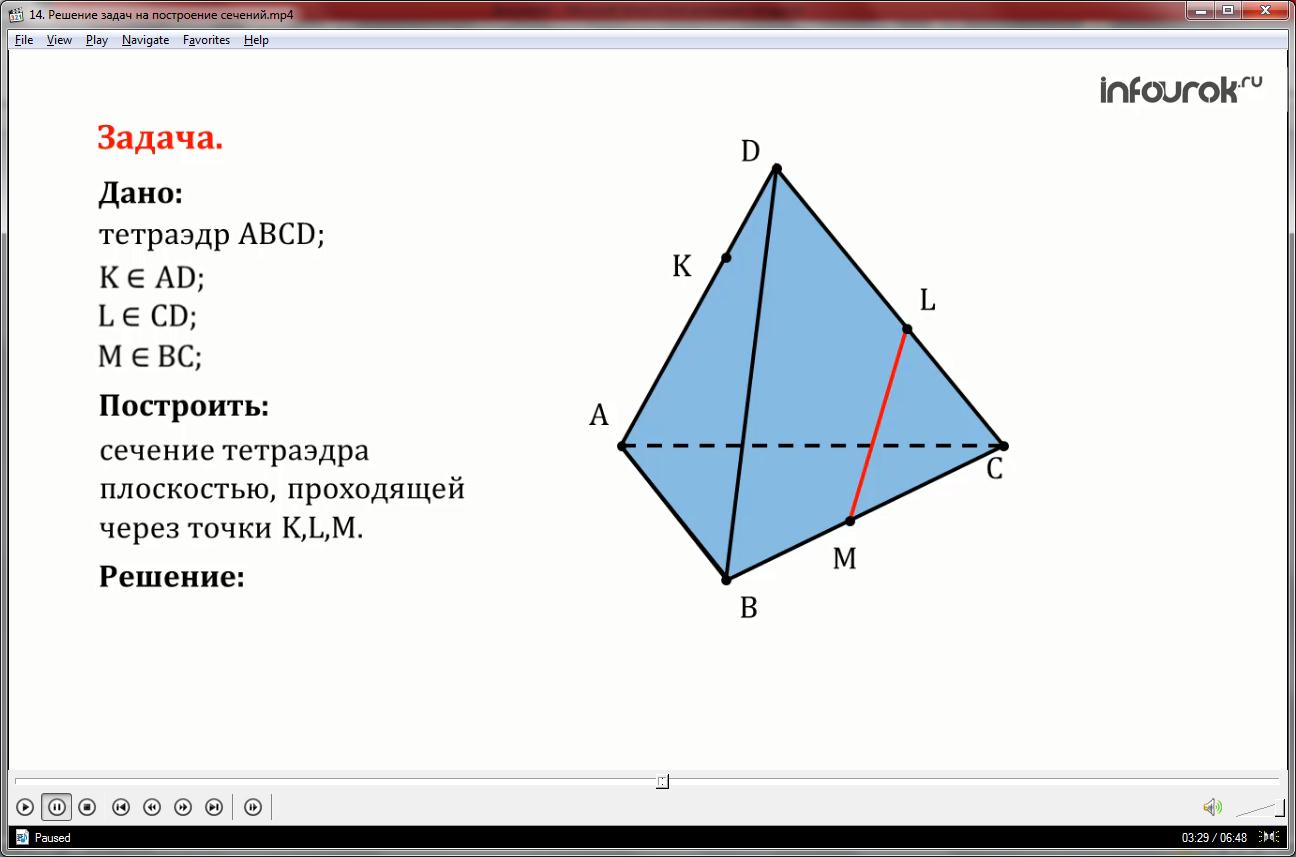
Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M.
Изобразим тетраэдр и данные точки.
При построении сечений нужно помнить один факт, что если две плоскости имеют общие точки, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Так у нас секущая плоскость проходит чрез точки M,L, а они лежат в плоскости CDB, значит ML-линия пересечения плоскостей.
Аналогично прямая KL является линией пересечения секущей плоскости и грани ADB
Для того чтобы построить линию пересечения с гранью АВС нужны две точки. Точка М уже у нас есть.
Для построения второй точки. Продлим до пересечения прямые KL и АВ. Отметим их общую точку S. Точка S принадлежит секущей плоскости, так как ей принадлежит прямая KL и принадлежит грани АВС, так как ей принадлежит прямая АВ. Значит секущая плоскость пересекает плоскость АВС по прямой MS.
Построим эту прямую. Отметим точку P- точку пересечения прямой с ребром АС. Отрезок PM- след от сечения грани плоскостью α.
Мы получили в результате две точки K и Р В грани АDC. Отрезок КР есть линия пересечения секущей плоскости и грани. Проведем этот отрезок.
Четырехугольник KLMP-искомое сечение.
Рассмотрим задачу на построение сечения параллелепипеда.

На рёбрах параллелепипеда даны точки K,L,M. Построить сечение параллелепипеда плоскостью KLM.
Построим данный параллелепипед и отметим указанные точки.
Так как точки L и M принадлежат грани АА1D1D и секущей плоскости, значит прямая LM их линия пересечения, а отрезок LM след от сечения грани АА1D1D секущей плоскостью.
Аналогично в грани DD1C1C построим прямую MK и выделим отрезок MK.
В грани А1B1C1D1 есть только одна точка L, для построения второй точки продлим до пересечения прямые D1C1 и MK. Отметим их общую точку H.
Точка H принадлежит секущей плоскости, так принадлежит прямой MK. И принадлежит грани A1B1C1D1, так как принадлежит прямой D1C1. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B1C1. Выделим отрезок LT это будет след от сечения плоскость.
Так как точки T и К принадлежат секущей плоскости и грани ВВ1С1С, то отрезок ТК будет следом от сечения в этой грани.
Выделим получившийся четырехугольник KMLT. Это искомое сечение.
Рассмотренные задачи относятся к классу задач на построение и имеют свои этапы решения: анализ, построение, доказательство. Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11621 |
| Номер материала | 928 |