
Урок «Сфера. Касательная плоскость к сфере»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем знакомство со сферой и её элементами.
На прошлом занятии вы изучили случаи взаимного расположения плоскости и сферы.
Следует помнить, что если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы данной плоскостью является окружностью.
Если расстояние от центра сферы до плоскости больше радиуса сферы, то плоскость и сфера не имеют общих точек.
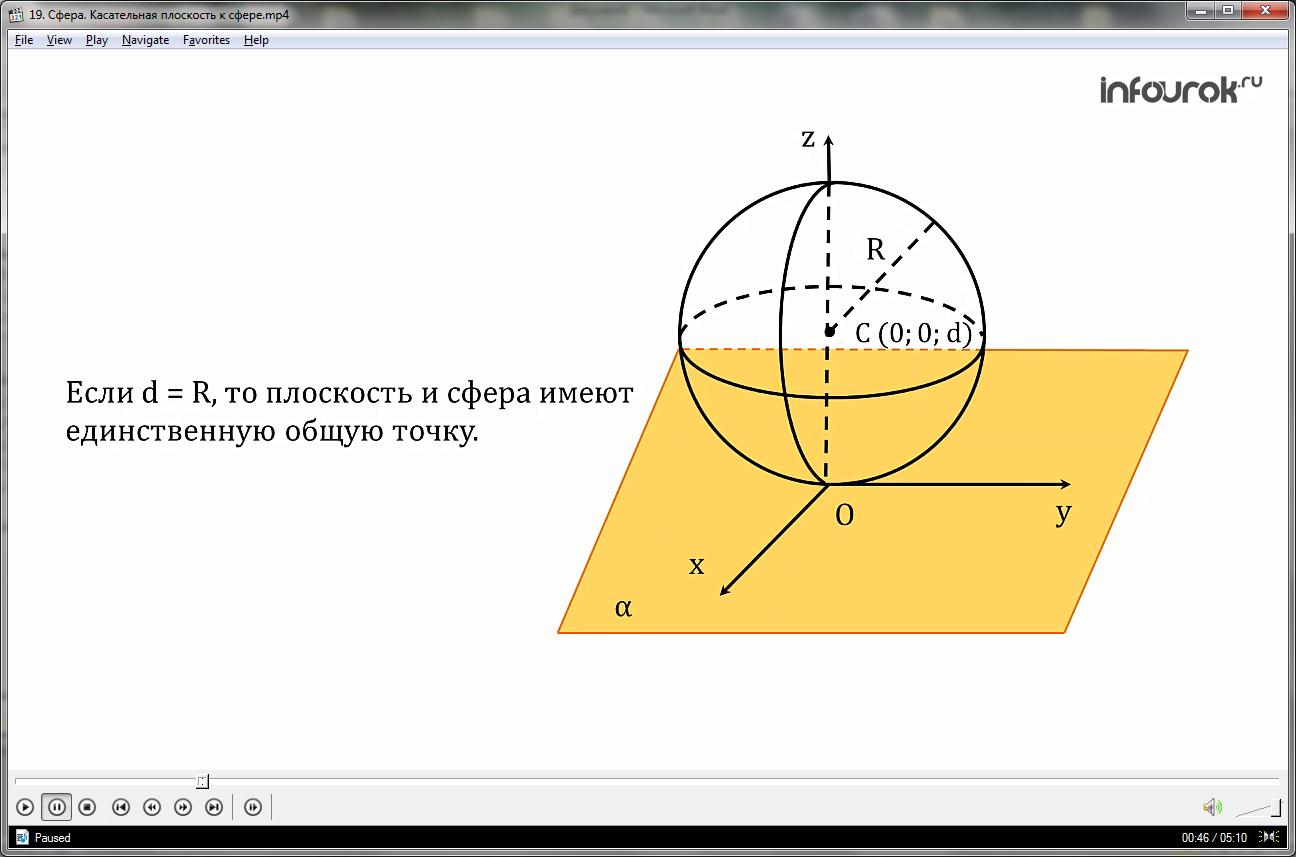
Если расстояние от центра сферы до плоскости равно радиусу сферы, то плоскость и сфера имеют единственную общую точку.
Рассмотрим подробно случай, когда плоскость и сфера имеют единственную общую точку.
Касательной плоскостью называется плоскость, имеющая со сферой только одну общую точку, данную общую точку называют точкой касания.
Рассмотрим касательную плоскость α к сфере с центром в точке О.
Докажем, что радиус сферы перпендикулярен касательной плоскости α.
1.Проведём доказательство методом от противного, то есть предположим, что радиус ОА не перпендикулярен касательной плоскости α.
2. Следовательно, ОА — наклонная к плоскости α, значит расстояние от центра сферы до плоскости α меньше радиуса ОА.
3. Таким образом, получили — сфера и плоскость α пересекаются по окружности, что является противоречием условию о том, что плоскость α и сфера имеют одну общую точку.

Следовательно, радиус ОА перпендикулярен к плоскости α.
Итак, мы доказали теорему о свойстве касательной плоскости к сфере: радиус сферы, перпендикулярен к касательной плоскости, если он проведён в точку касания плоскости и сферы.
Данное свойство аналогично свойству касательной к окружности.
Докажем обратную теорему.
1.Проведём радиус сферы перпендикулярно к плоскости, проходящей через его конец.
2.Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, значит, плоскость и сфера имеют только одну общую точку, следовательно, данная плоскость является касательной к сфере.
Таким образом, мы доказали, что если радиус сферы перпендикулярен к плоскости, проходящей через его конец, то эта плоскость является касательной к сфере.
Применим полученные знания при решении задач.
Задача 1.
Радиус сферы равен 112 см. Точка, лежащая на плоскости касательной к сфере, удалена от точки касания на 15 см. Найти расстояние от этой точки до ближайшей к ней точки сферы.
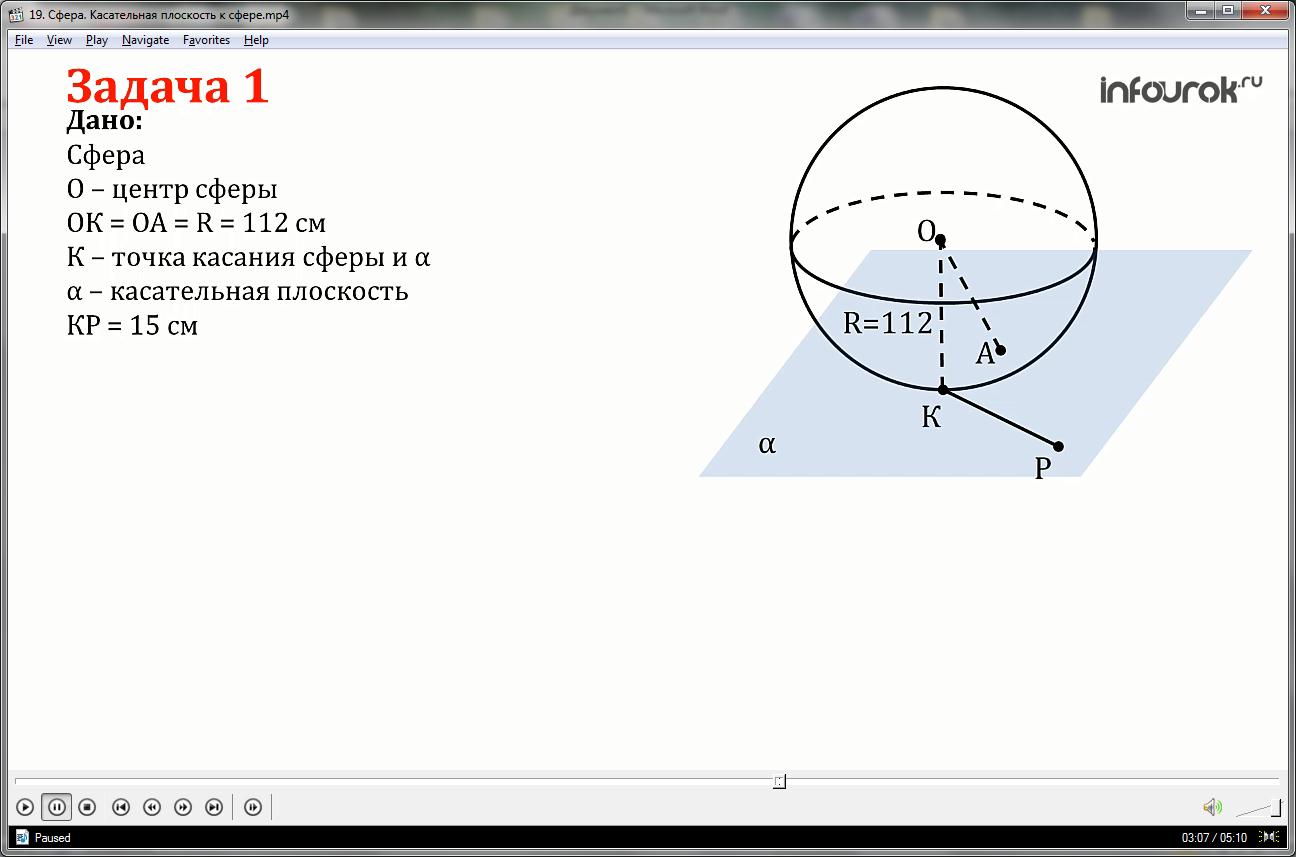
1)Докажем, что точка А принадлежащая отрезку ОР, будет ближайшей к точке Р.
Выберем произвольную точку N на сфере.
Проведём отрезки NO и NP.
Из неравенства треугольника ONP следует:
ON+NP OP.
ОА+АР=ОР, тогда
ON+NP OA+AP, где ON и OA это радиусы.
Следовательно, R+ NP R+АР или NP АР.
Итак, АР NP, а так как точка N выбрана произвольно, то точка А, принадлежащая отрезку ОР, будет ближайшей к точке Р.
2.Найдём длину искомого отрезка АР как разность отрезков ОР и ОА, где ОА радиус сферы R.
По известной теореме радиус сферы, перпендикулярен к касательной плоскости, если он проведён в точку касания плоскости и сферы, имеем, что треугольник ОКР — прямоугольный.
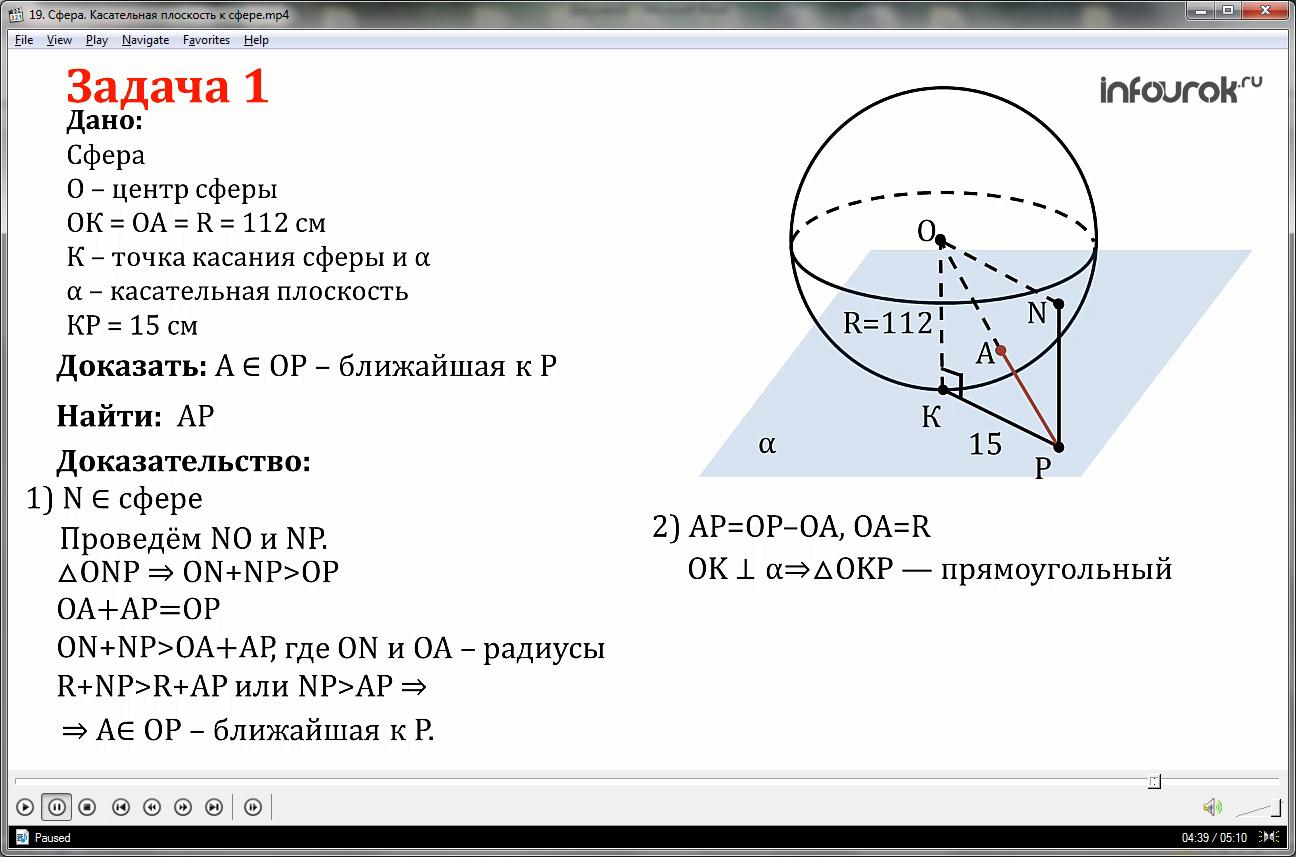
Отрезок ОР является гипотенузой данного треугольника, найдём его по теореме Пифагора:
ОР=√ОК2+КР2=√1122+152=√12544+225=√12769=113 см
Итак, АР=ОР-ОА=113-112=1 см.
Таким образом, расстояние от точки, лежащей на плоскости касательной, к сфере до ближайшей к ней точки сферы равно 1 см.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 14628 |
| Номер материала | 1005 |