
Урок «Сфера. Площадь сферы»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Продолжаем изучение сферы.
На прошлых занятиях вы познакомились с определением касательной плоскости к сфере, её свойством, а так же с признаком касательной плоскости к сфере.
Итак, касательной плоскостью называется плоскость, имеющая со сферой только одну общую точку, данную общую точку называют точкой касания.
Вспомним, что радиус сферы перпендикулярен касательной плоскости, если он проведён в точку касания плоскости и сферы.

Сферу нельзя развернуть на плоскость, в отличие от боковой поверхности цилиндра или конуса, поэтому здесь непригоден способ вычисления и определения площади поверхности с помощью развёртки.
Воспользуемся понятием описанного многогранника для определения площади сферы.
Итак, многогранник называется описанным около сферы, если сфера касается всех его граней, другими словами плоскость каждой грани является касательной к сфере.
В этом случае сфера — вписанная.
Пусть описанный около сферы многогранник имеет k граней.
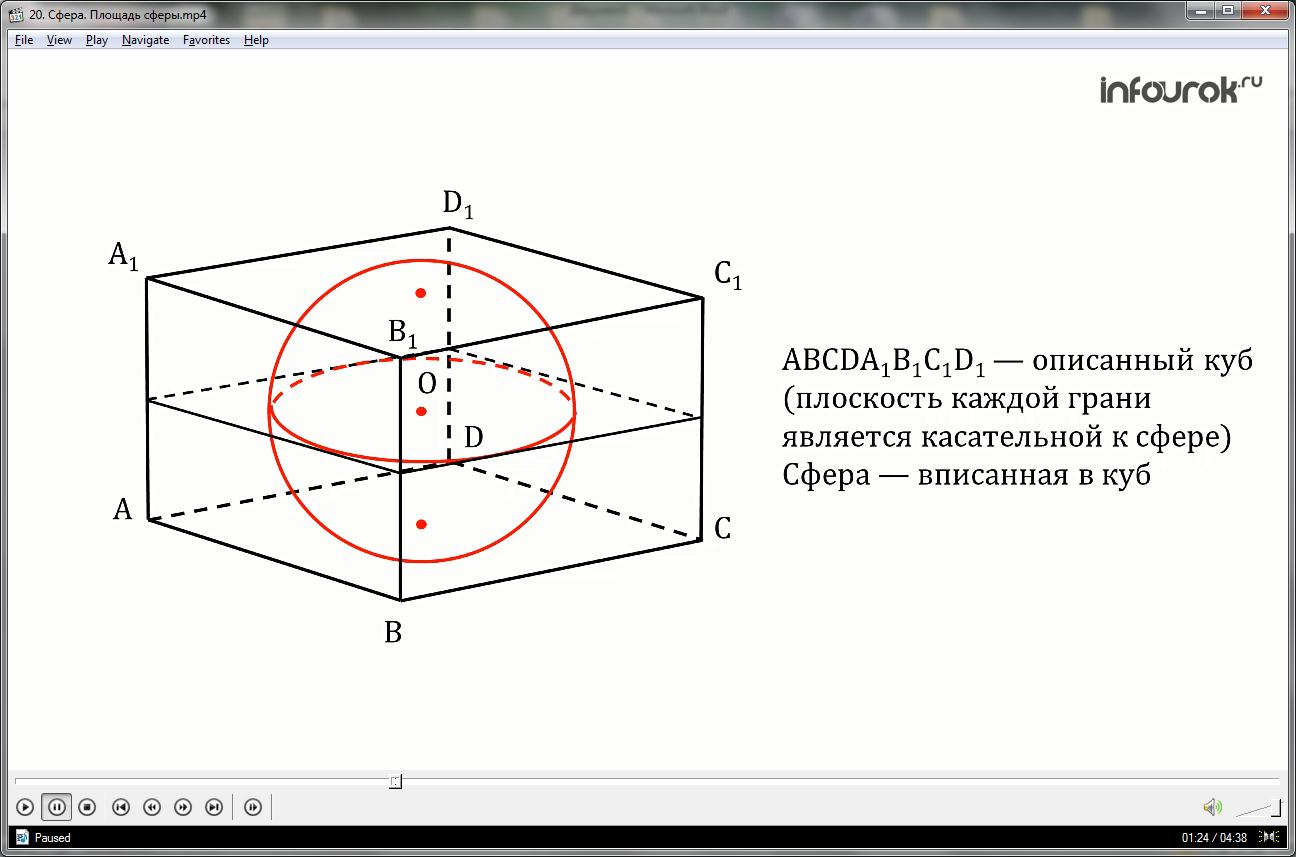
Если неограниченно увеличивать число k граней так, чтобы наибольший размер каждой грани стремился к нулю, то за площадь сферы можно принять предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.
При дальнейшем изучении темы «Площадь сферы», мы докажем существование этого предела, а так же выведем следующую формулу для нахождения площади сферы радиуса R:
S=4 R2
Применим полученные знания при решении задач.
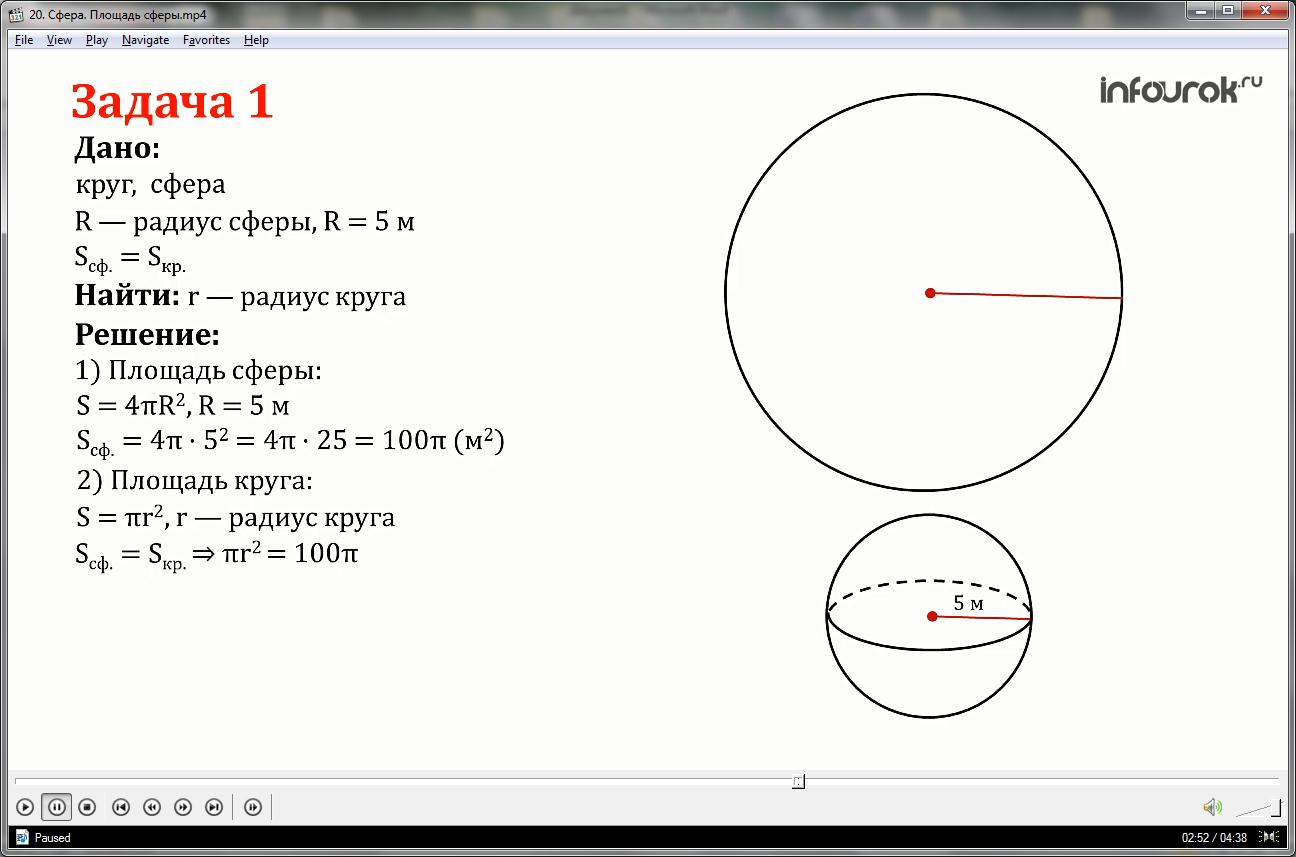
Задача 1.
Вычислить радиус круга, площадь которого равна площади сферы с радиусом 5 м.
Решение:
1. Площадь сферы вычисляется по формуле:
S=4 R2, радиус сферы равен 5 м.
Таким образом, площадь сферы равна:
S=4 *52=4 *25=100 (м2)
2.Площадь круга вычисляется по формуле:
S= r 2, где r-радиус круга.
Из условия известно, что площадь сферы равна площади круга, то есть r 2=100
r 2=100, следовательно r =10 (м).
Таким образом, радиус круга, площадь которого равна площади сферы радиуса 5 м, равен 10 м.
Задача 2.
Сечение шара площадью 16 см2 находится на расстоянии 3 см от центра шара. Найти площадь поверхности шара (сферы).
Решение:
1.Сечение сферы является кругом, площадь которого вычисляется по формуле:
S= r 2=16 , где r=АВ — радиус круга.
Найдём радиус сечения r:
r=√ =√16, r=АВ=4 (см)
2.Рассмотрим треугольник ОАВ:
ОА=d — расстояние (перпендикуляр) от центра шара до сечения.
Значит, угол А равен 900.
Таким образом, из прямоугольного треугольника ОАВ по теореме Пифагора находим отрезок ОВ, который является радиусом сферы:
ОВ= R=√АВ2+ОА2=√42+32=√25=5 (см)

3.Площадь сферы вычислим по формуле:
S=4 R2, где R — радиус сферы.
Sсф=4 *52=4 *25=100 (см2)
Ответ: Sсф=100 см2
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 13356 |
| Номер материала | 1006 |