
Урок «Сфера. Уравнение сферы»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Продолжаем изучение сферы.
На прошлых занятиях вы познакомились с определением сферы и шара.
Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.
Данная точка — центр сферы.
Заданное расстояние — радиус сферы.
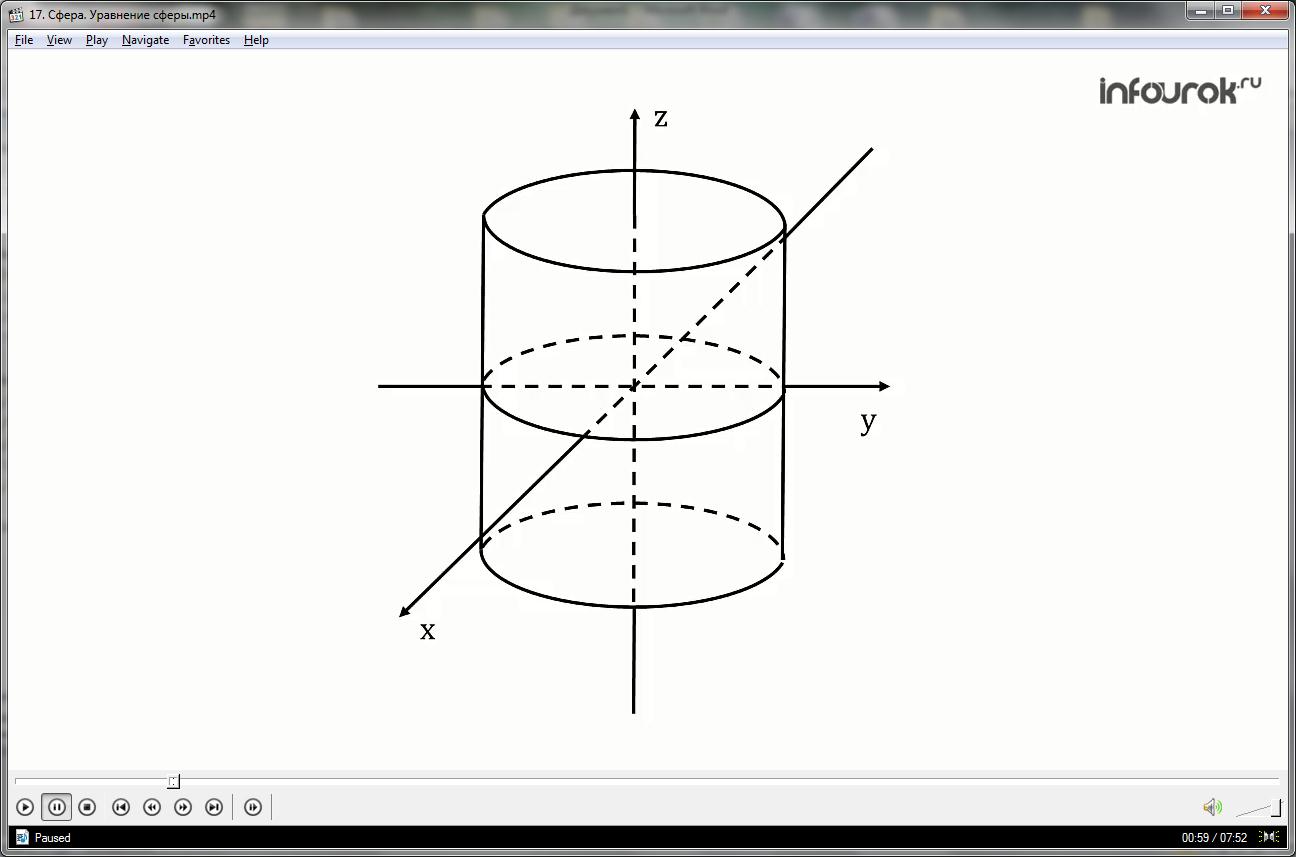
Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.
Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).
2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.
МС=√(x-x0)2+(y-y0)2+(z-z0)2.
3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть
R=√(x-x0)2+(y-y0)2+(z-z0)2 или
R2=(x-x0)2+(y-y0)2+(z-z0)2 .
4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.
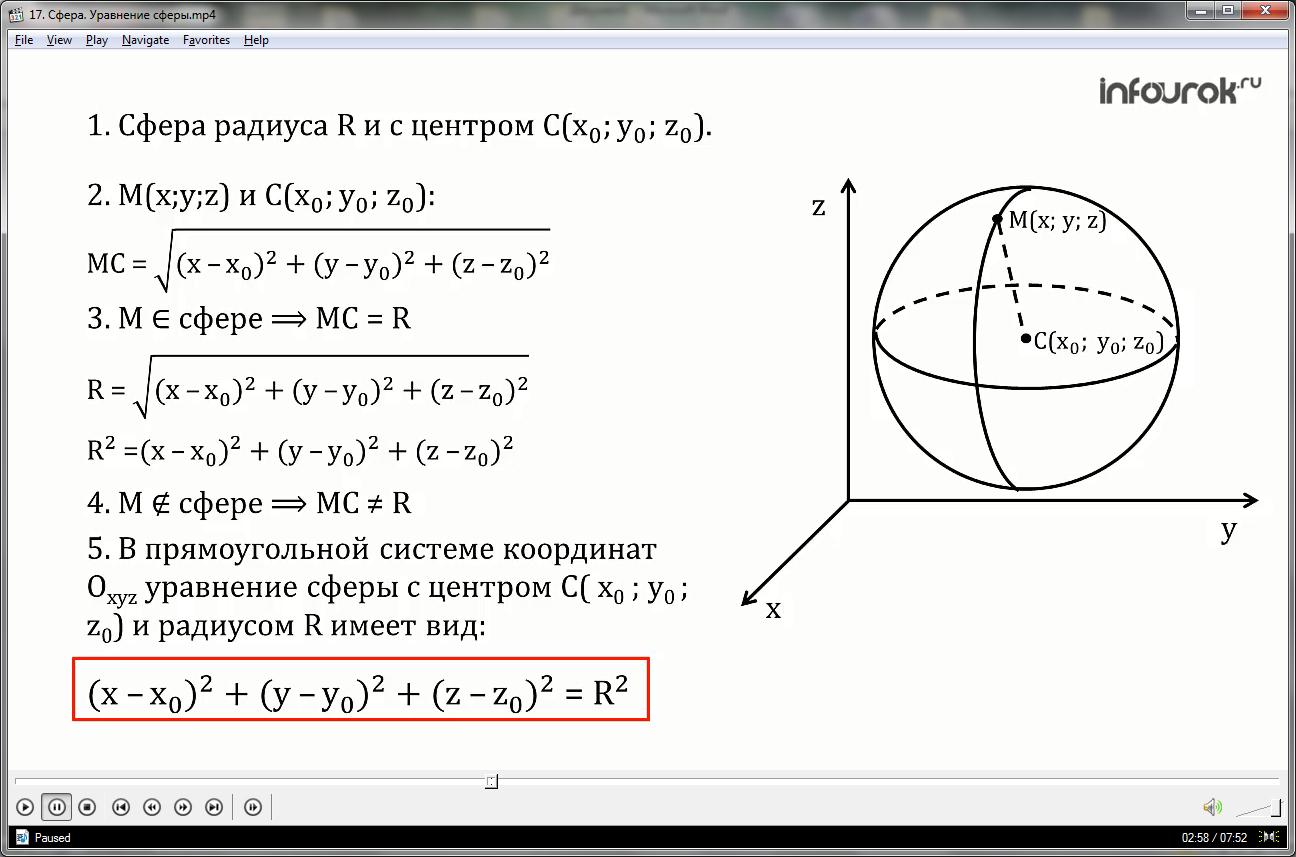
5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром
С (x0 ; y0 ; z0) и радиусом R имеет вид:
(x-x0)2+(y-y0)2+(z-z0)2 = R2
Применим полученные знания при решении задач.
Задача 1.
Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).
Решение:
1.Запишем уравнение сферы с центром
А (x0 ; y0 ; z0) и радиусом R:
(x-x0)2+(y-y0)2+(z-z0)2 = R2
2.Подставим соответствующие координаты центра сферы А в данное уравнение:
(x+2)2+(y-2)2+(z-0)2 = R2
Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:
(x+2)2+(y-2)2+z2 = R2
3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:
R2=(5+2)2+(0-2)2+(-1)2 =49+4+1=54
Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:
(x+2)2+(y-2)2+z2 = 54
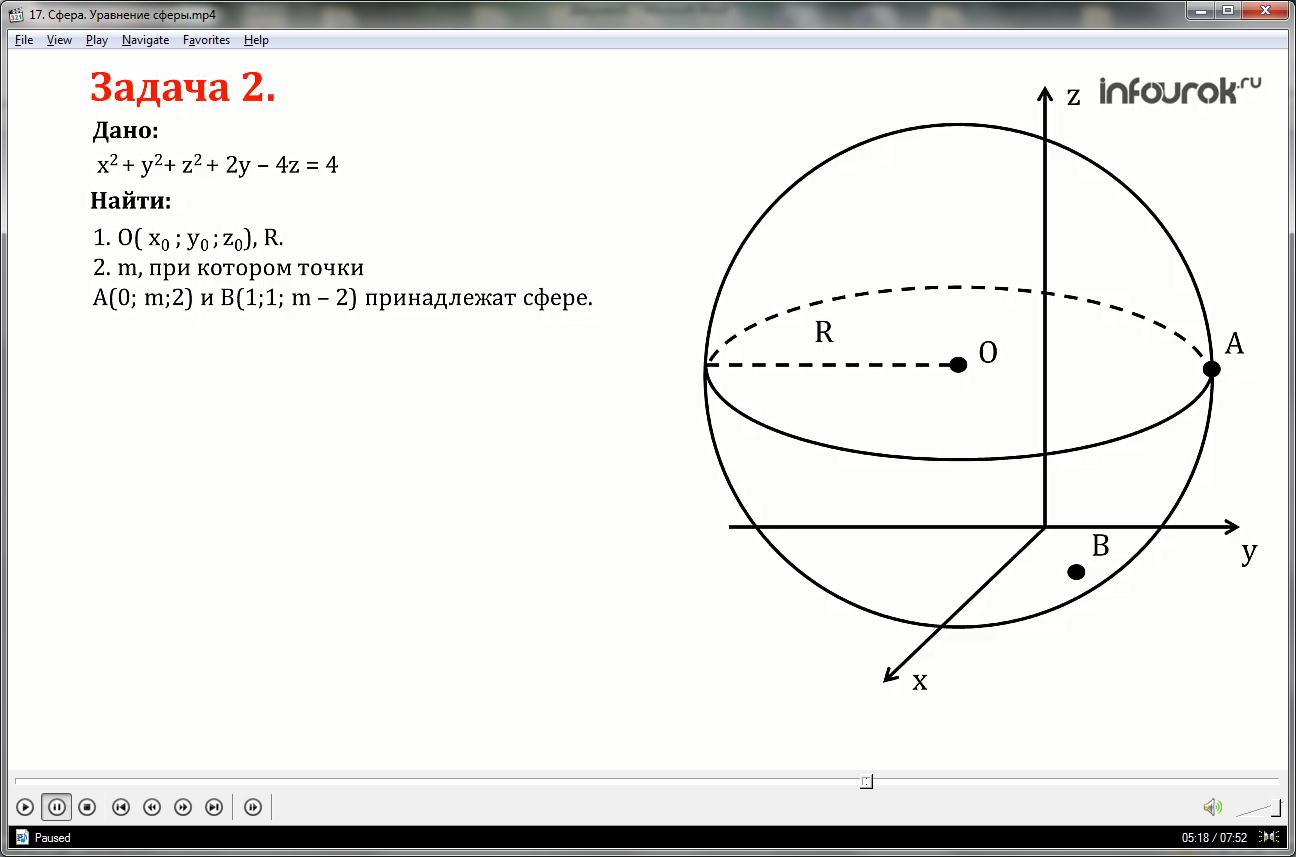
Задача 2.
Сфера задана уравнением:
x2+ y2+ z2+2y-4z=4
1) Найти координаты центра и радиус сферы;
2) Найти значение m, при котором точки
А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.
Решение:
1. Уравнение данной сферы имеет вид:
x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4
Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:
x2+ y2+2y+1-1 + z2-4z+4-4=4
Уравнение примет вид:
x2+( y+1)2+( z-2)2-5=4 или
x2+( y+1)2+( z-2)2=9
Таким образом, центр сферы имеет координаты:
О (0;-1;2), радиус равен R=√9=3
2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:
x2+( y+1)2+( z-2)2=9
Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:
02+( m+1)2+(2-2)2=9
12+(1+1)2+( m-2-2)2=9
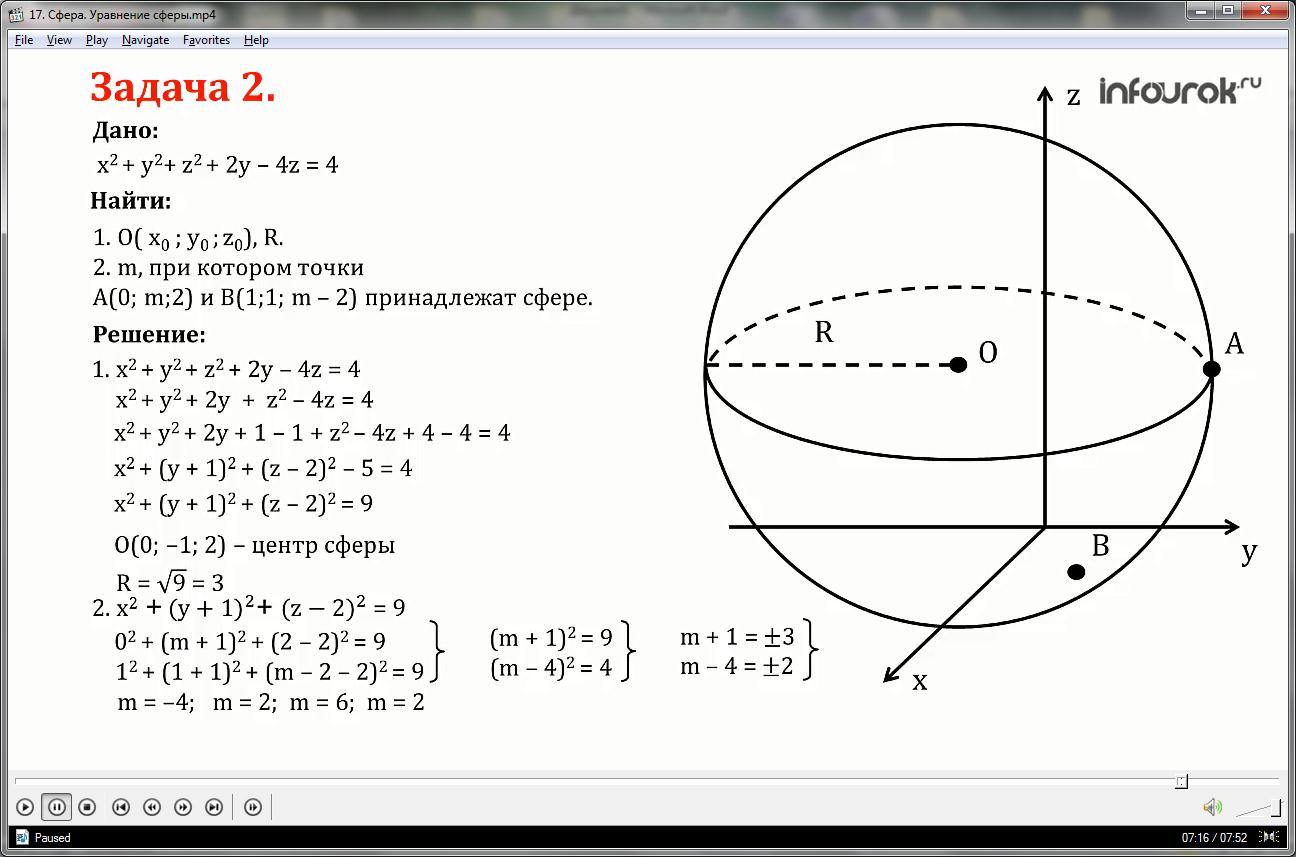
Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:
Таким образом, мы получили 4 значения m:
m=-4; m=2; m=6; m=2.
Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.
Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением
x2+ y2+ z2+2y-4z=4 с центром в точке
О (0;-1;2) и радиусом R=3.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 73356 |
| Номер материала | 1003 |